獨立數

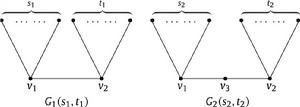
圖論內的概念之一。設圖G=(V,E),V(G),E(G)圖G的頂點集和邊集.獨立數α指的是圖G中頂點獨立集最大基數，對於不同α的值，對應有不同的特殊圖，我們可以通過研究圖的鄰接矩陣，拉普拉斯矩陣，無符號拉普拉斯矩陣來研究一些特殊圖的結構。

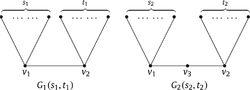
1

例如：S1+t1=n-2

s2+t2=n-3

在簡單圖中可以這樣定義：設S是V(G)的非空子集，若S中任意兩點均不相鄰，則稱S為G的一個獨立集，又若不存在G的獨立集P，使得|P|>|S|，則稱S為G的最大獨立集，此時記 α(G)=|S|，稱α(G)為G的（點）獨立數