簡介
特徵標是一種特殊函式,即群G的與它的某個線性表示有密切關係的函式。
設ρ:G→GL(V)是群G的一個F線性表示。取定V的一個基,並假定在這一基下ρ對應的矩陣表示為T:G→GL(F)。對g∈G,記tr(T(g))為矩陣T(g)的跡,即T(g)的主對角線元素之和。定義G上的F值函式(g)=tr(T(g)),g∈G,其取值與v的基選擇無關,稱這一函式為P所提供的F特徵標。
通常把複數域上表示對應的特徵標稱為復特徵標。
性質
特徵標是群G上的類函式,即其取值在G的同一個共軛類上相同。
類函式
 特徵標
特徵標在數學中,一個 類函式是指關於函式組共軛類的不變函式。換句話說,它在 G上的共軛映射不變。這些函式在群論、組表示中占有基礎地位。
 特徵標
特徵標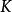 特徵標
特徵標 特徵標
特徵標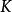 特徵標
特徵標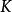 特徵標
特徵標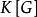 特徵標
特徵標若為有限群,是一個域,則在場上線性表示的特性總是一個類函式,其值為,此時類函式構成群代數的中心。
