熱力學本構方程

熱力學本構方程Helmholtz 自由能或者利用Gibbs自由能來實現的方程，主要套用於形狀記憶聚合物（SMP）的研究。基於不同預應變率下的熱力學實驗結果，通過考慮材料凍結/恢復過程中的時間延遲效應 、應力鬆弛效應以及熱變形效應的影響，對其凍結和恢復回響進行理論分析。

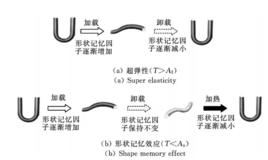
建立的有效途徑

根據熱力學基本原理，熱力學本構方程有兩個有效途徑：一是利用Helmholtz 自由能；二是利用Gibbs自由能。

套用

主要用於形狀記憶聚合物變形機理研究：從微觀結構看，形狀記憶材料可以理解為由凍結態和激活態組成的兩相結構，其凍結過程對應激活態逐步轉變為凍結態的過程，而恢復過程則對應微結構由凍結態向激活態的轉變過程。任一時刻凍結態體積份數φf(T)、激活態體積份數φα(T)和等效模量E(T)可分別表示為：

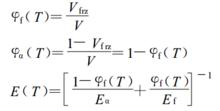熱力學本構方程

式中：V凍結態體積份數；V—材料總體積；E和E—激活態和凍結態楊氏模量。

隨著溫度的降低，應力幅值由三部分組成：初始預應力，降溫過程中的熱應力累積，以及由於粘性效應造成的機械和熱應力損失。因此，其應力表達式為：

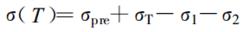熱力學本構方程

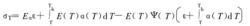熱力學本構方程

熱力學本構方程是形狀記憶聚合物變形機理研究的基礎，基於形狀記憶聚氨酯單軸拉伸和三點彎曲實驗結果，對其形狀凍結和恢復過程進行了理論分析，在此基礎上，建立了一個新的熱力學本構方程。該模型通過引進等效延遲係數考慮了材料形狀凍結/恢復時間延遲效應，通過引入應力鬆弛係數考慮了材料粘彈效應的影響。