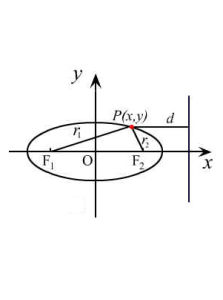
橢圓的焦半徑公式
 焦半徑公式
焦半徑公式設M(m ,n)是 橢圓x^2/a^2+ y^2/b^2=1(a>b>0)的一點,r1和r2分別是點M與點F₁(-c,0),F₂(c,0)的距離,那么(左 焦半徑)r₁=a+em,(右焦半徑)r₂=a -em,其中e是離心率。
推導:r₁/∣MN1∣= r₂/∣MN2∣=e
可得:r1= e∣MN1∣= e(a2/ c+m)= a+em,r2= e∣MN2∣= e(a2/ c-m)= a-em。
同理:∣MF1∣= a+em,∣MF2∣= a-em。
所以:橢圓通徑=(2·b^2)/a
雙曲線的焦半徑公式
1:定義:雙曲線上任意一點P與雙曲線焦點的連線段,叫做雙曲線的 焦半徑。
2.已知雙曲線標準方程x^2/a^2-y^2/b^2=1
點P(x,y)在左支上
│PF1│=-(ex+a) ;│PF2│=-(ex-a)
點P(x,y)在右支上
│PF1│=ex+a ;│PF2│=ex-a
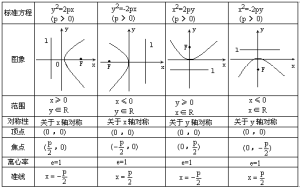
拋物線的焦半徑公式
拋物線r=x+p/2
通徑:圓錐曲線(除圓)中,過焦點並垂直於軸的弦
雙曲線和橢圓的通徑是2b^2/a 焦準距為a^2/c-c
拋物線的通徑是2p
拋物線y^2=2px (p>0),C(Xo,Yo)為拋物線上的一點,焦半徑|CF|=Xo+p/2.