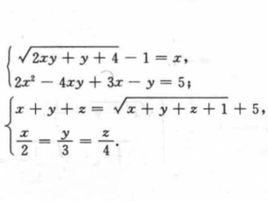基本介紹
解無理方程組的基本思想方法是把它轉化為有理方程組來解,解無理方程組時,由於方程的變形可能會產生增根,因此解無理方程組必須驗根。
解無理方程組時,可以利用解無理方程的一些基本方法,將方程組化為有理方程組來求解。不論採用什麼方法,其目的都是要化繁為簡,減少方程中未知數的個數,或降低未知數的次數。必須注意,當無理方程轉化成有理方程求得解後,要及時進行檢驗,捨去不合題意的根,以減少不必要的運算與錯誤 。
例題解析
【例1】解下列方程組:
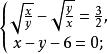 無理方程組
無理方程組①
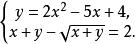 無理方程組
無理方程組②
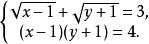 無理方程組
無理方程組③
解:①
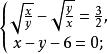 無理方程組
無理方程組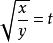 無理方程組
無理方程組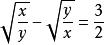 無理方程組
無理方程組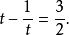 無理方程組
無理方程組設,則方程可化為
整理得
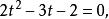 無理方程組
無理方程組解得
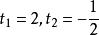 無理方程組
無理方程組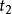 無理方程組
無理方程組其中不合題意捨去。所以
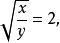 無理方程組
無理方程組即
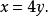 無理方程組
無理方程組解方程組
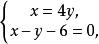 無理方程組
無理方程組得
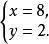 無理方程組
無理方程組經檢驗,原方程組的解為
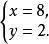 無理方程組
無理方程組②
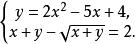 無理方程組
無理方程組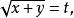 無理方程組
無理方程組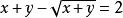 無理方程組
無理方程組設則方程可化為
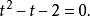 無理方程組
無理方程組解得
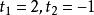 無理方程組
無理方程組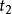 無理方程組
無理方程組其中不合題意捨去,所以
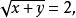 無理方程組
無理方程組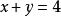 無理方程組
無理方程組即。
解方程組
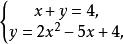 無理方程組
無理方程組得
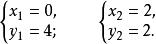 無理方程組
無理方程組經檢驗,原方程組的解為
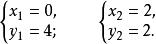 無理方程組
無理方程組③
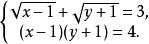 無理方程組
無理方程組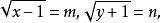 無理方程組
無理方程組設則原方程組可化為
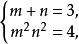 無理方程組
無理方程組即
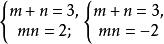 無理方程組
無理方程組其中
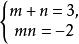 無理方程組
無理方程組不合題意捨去。解方程組
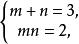 無理方程組
無理方程組得
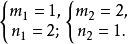 無理方程組
無理方程組所以
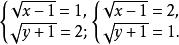 無理方程組
無理方程組解得
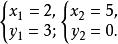 無理方程組
無理方程組