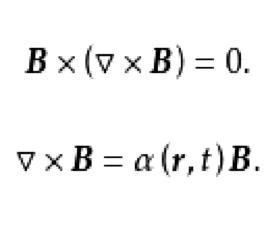磁場的經驗分布
人們知道，磁場廣泛地控制著太陽大氣的結構和動力學過程。尤其是，在太陽活動中，磁場的作用就更為明顯。具體地講，對於太陽射電磁迴旋輻射的研究，磁場是一個基本且重要的關鍵物理參數，例如它在微波爆發的迴旋同步加速輻射的發射機制中就扮演了一個決定性的角色。
最可靠的太陽磁場測量，是來自光球層的Fraunhofer線的Zeeman分裂的光學觀測。可是，迄今為止，還沒有像測量光球磁場一樣的直接方法，來測量高層大氣中的磁場。
對於磁場的估算，除了光學和紫外觀測而外，射電觀測就是最有效的途徑。為了要推導出關於磁場的信息，幾乎利用了所有種類的太陽射電輻射的有關特性，例如，可以通過微波爆發的頻譜和偏振來進行分析。
Dulk和McLean對活動區上空日冕中磁場強度的觀測證據進行了評論，並且根據當時(70年代)最新的實際觀測資料，依照電漿理論，確定出哪些資料更為可靠，從而對以前的一些磁場強度的估計作了修正，他們發現從各個不同的途徑所得到的結果大體上是一致的，依據並概括了所有這些資料，而擬合出活動區日冕磁場強度的經驗公式：
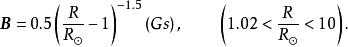無力場式中R為日心距離，該公式對整個觀測資料都相當精確，不會超過兩倍，而且，它是個單參數函式，用起來極為方便 。
無力場基本介紹
通常用來從理論上外推到太陽高層大氣(例如日冕)中的磁場的模型，就是所謂“ 無作用力磁場”(簡稱 無力場)。由磁流體力學可知，只要電流方向與磁場方向平行，Lorentz力就為零，因此，產生無力場的條件是
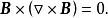無力場換句話說，滿足條件
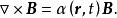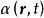無力場
無力場的磁場就是 無力場。對於滲透進磁場的電漿，只有當其磁力遠大於其它力時，才有可能維持這種無力場。標量稱為 無力因子，它一般為空間和時間的函式，它是磁力線扭轉的一種量度，並正比於在磁場方向上流動的電流。
無力場 無力場如果無力因子為常數，那么這時的無力場就被稱為 穩定無力場，它表征此時的系統是處於最小磁能狀態。在太陽大氣電漿(色球和日冕)中，由於密度非常小，因而氣體壓力和重力比磁壓力小得多，所以其磁場可以被看作無力場位形。這樣，只要所討論的局部磁化電漿不是處於活動性非常強的活動區中，我們總可以用這種常無力場作為瞬時的真實的磁場結構的近似，而來進行外推。
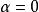無力場如果無力因子，那么
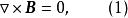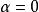無力場 無力場這表明磁場的旋度為零，因而磁場是一個無旋場，或者有勢場。通常，我們稱其旋度為零的磁場為無電流場，或者勢場，顯然，無電流場是無力場的一種特殊情況()，此時的磁場能量當然是處於最低狀態，而且磁力線沒有扭轉。勢場的位形比較簡單，它表征了一般無力場的某種平均特性。
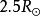無力場對於低於的內冕區域以及其中的活動區精細結構，完全可以用這種勢場來近似表達真實的磁場位形。尤其是，對小尺度日冕磁結構，其計算結果和觀測資料相當一致。因此，只要活動區不是處於急劇上升或下降的階段，我們就可以用勢場模型來外推內冕區域(這裡也正是微波爆發起源的地方)中的磁場。
無力場利用勢場位形，是很容易外推而得到色球和內冕中的磁場的。我們知道，在給定的初始邊界條件下，由矢量場的旋度和散度，便可唯一地求出這個矢量場。由勢場的充要條件(1)可知，磁場 B定是某標量的梯度，即
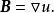無力場另外，因為磁場為無源場，故其散度為零，即
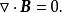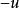無力場
無力場因此， B既是勢場，又是無源場，那么它必定是個調和場，而調和場的勢函式()滿足Laplace方程
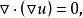無力場即
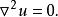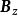無力場
無力場這樣，如果在一個基本表面上垂直分量的分布已知的話，那么就可以計算出磁場 B了。例如，有人就曾假設該基本表面為一平面，而計算過太陽上某些區域中的磁場；也有人以整個太陽光球層作為該基本表面進行過太陽大氣中的磁場計算；這樣，就分別得到了描述太陽大氣磁場分布的精細結構以及總體結構。
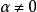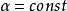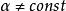無力場
無力場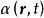
無力場 無力場儘管上述勢場外推法比較方便，但是它畢竟是第一近似，進一步，應該採用但的穩定無力場(又稱線性無力場)；以及更進一步，乃至應該採用，而為變數的一般無力場(又稱非線性無力場)。為了獲得較高程度的近似，這些計算將會變得更加複雜，而且要求附加的信息(或者假設)，來確定無力因子的分布，估計其數值 。
