定義
激波裝配法是雙曲型方程數值解法中處理激波的一種方法。即在間斷面兩側區域分別滿足方程,激波兩邊作為邊界條件,其物理量由激波的Hugoniat關係相關聯,且將激波作為待定的運動邊界。
簡介
激波裝配法(shock-patching method)一種激波數值處理方法。它把激波當做未知的運動邊界,按照激波間斷條件—R-H激波關係式把激波分離出來,準確算出激波位置,在光滑區用近似方法求解微分方程,而在間斷處用R-H關係式求解.激波裝配法具有精度高,激波位置精確,物理圖象清楚等優點.但計算十分繁複,因此它只適用於那些激波運動情況較簡單,流場圖案清楚的流動。
發展歷史
激波是可壓縮流體動力學中最重要的物理現象,模擬激波自然也構成計算流體力學(CFD) 主要的研究內容。激波的模擬方法分為捕捉和裝配兩種。1953年,Lax提出自動捕捉雙曲型守恆率方程間斷解的一階格式,在套用中發現數值解存在非物理波動;1959年,Godunov基於弱解理論,利用間斷滿足的 Riemann分解的特性,構造出物理背景清晰計算穩定的一階格式。由於這兩種格式都只有一階精度,計算得到的激波需要若干格線點過渡 ( 所謂激波較寬)。直到1983年Harten提出TVD格式才實現二階精度,使得激波解析度得以提高。其後發展了許多高精度格式,如NND、ENO、WENO等,近幾年三階乃至更高階的WCNS也得到實際套用。1966年,Moretti根據激波上下游流動參數滿足 R-H關係式的特點提出激波裝配法,高精度高效率地模擬出鈍體頭部脫體激波,二維情況下裝配法使用10 ×16個格線得到的壓力分布的精度不遜於當代捕捉法使用385 ×513個格線的精度,極大地推動了當時超聲速流動的套用研究,直到上世紀80年代後期依然是主流算法。然而,這種算法需要事先確定激波位置,套用受到極大限制,隨著高精度捕捉法的發展,裝配法的研究熱情逐漸消退。
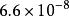 激波裝配法
激波裝配法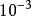 激波裝配法
激波裝配法激波空間尺度只有幾個分子的平均自由程。在海平面標準狀況下,馬赫數M=2.95的正激波厚度大約為,而常見的飛行器在10m量級,目前航天航空領域CFD套用中量級格線很少見,因此採用捕捉方法模擬出來的激波寬度要比實際的激波厚度大得多。激波內部處於熱力學非平衡狀態,而建立Euler或NS方程時採取了熱力學局部平衡假設、密度不存在劇烈變化的Stokes假設以及採用了忽略鬆弛時間的狀態方程等,從理論角度看,從Euler或NS方程出發捕捉激波,即使未來幾十年後計算機發展使得激波厚度內布置若干格線成為常態,只要過度區有1個格線點,也會產生非物理波動。描述激波最完善的數學理論是雙曲型守恆率方程的弱解理論。它把激波看作無厚度的間斷,流動參數在此發生突躍。
由於捕捉法計算激波存在諸多理論缺陷,Moretti G認為捕捉法經過36年(1966 2001)的發展依然無法超越裝配法。近幾年國外一些學者重新審視裝配法,解決了高精度格式套用於高馬赫數流動時在激波附近出現波動的問題 Paciorri等人採用在捕捉法得到的流場基礎上裝配浮動激波的新思路突破傳統裝配法的限制,極大推動了套用領域拓展。浮動激波裝配法通過局部格線重構來形成內部激波邊界,由於激波運動以後需要在背景格線上重新定位和插值,流場信息傳遞使其難以用於非定常流動。
非結構格線與激波裝配法
激波裝配法是由Gino Moretti在20世紀60年代提出的。激波裝配法包含兩部分內容:激波運動速度和激波上下游參數的確定。除了Moretti之外,還有一些其他學者在後來套用該方法進行了研究。當時由於激波裝配方法對於強間斷激波的高分辨特性備受青睞。然而,在90年代隨著激波捕捉方法以及計算機的的發展,Moretti等人採用的基於結構格線的激波裝配方法,由於其算法的複雜性和操作的困難性,對其研究的熱情也一度消退。
從20世紀90年代初,基於非結構格線的數值模擬受到越來越多學者的關注。這主要是因為以下兩個重要的特點:(1)對於複雜幾何外形的描述能力;(2)具有局部調整格線來體現流動特點的可能性。非結構格線技術的出現和發展也為激波裝配方法的套用提供了一個新的契機。
傳統激波裝配方法基於邊界激波和浮動激波兩種概念。邊界激波是將激波看作邊界,計算區域被分成若干子區域,激波點就是邊界格線點。浮動激波是激波點在一個背景格線上進行運動。由於浮動激波點並非格線點,所有存在激波點和格線點之間的插值問題。這兩種方法出發點不同,相對而言激波邊界方法更容易實現。
無論是邊界激波方法還是浮動激波方法都涉及到格線的運動,因此動格線技術是其不可缺少的技術手段。
優點
激波的計算方法大體可以分為激波捕捉和激波裝配兩種。捕捉方法無需事先知道激波位置,激波是在計算過程中自動得到的。這種方法如果沒有特殊處理,數值解會在激波附近產生非物理振盪[’]。儘管激波捕捉方法在過去20多年得到廣泛研究和迅速發展,但其仍存在很多問題,如精度、穩定性等。而且這些問題很容易出現在基於非結構格線的高超聲速流動計算中。相對激波捕捉方法,激波裝配方法由於不存在這些數值問題,對其研究也是具有很大的實際意義。

