簡介
由於滾動接觸問題的系統研究始於輪軌接觸問題的研究，當前常用的滾動接觸問題解決方法多來自輪軌接觸研究領域，因此，下面主要介紹輪軌滾動接觸理論。輪軌滾動接觸理論（theory of wheel-rail rolling contact）研究輪軌滾動接觸行為的理論。輪軌滾動接觸理論是研究列車運行時，輪軌相對運動狀態和接觸斑上作用力的關係。接觸斑上的作用力包括其大小、方向和分布。
接觸理論的創始人是Hertz Heinrich，1882年他在德國一家雜誌上發表了具有開創性的論文“論彈性固體的接觸”。他對接觸問題的研究起因於對玻璃間光學干涉的試驗，兩個軸線成45°的圓柱形玻璃透鏡受壓後發生彈性變形，從彈性變形對干涉條紋圖像存在的影響提出了接觸壓力呈橢圓形分布的假設。這一結論一直在鐵路輪軌、齒輪、軸承等工業的發展中起著重要的作用。實際上Hertz理論作了如下簡化：接觸物體被看作彈性無限半空間，接觸載荷僅僅作用在平面上一個小的橢圓區域上，接觸體內在接觸區附近應力分布是高度集中的，並和物體接觸區附近的幾何尺寸有關。這就要求接觸區幾何尺寸遠小於物體的幾何特徵尺寸和接觸區附近的曲率半徑。Hertz在研究中，又假設接觸表面是光滑的，無摩擦效應，接觸物體表面僅傳遞法向力。Hertz接觸理論為後來的接觸理論及滾動接觸理論的發展奠定了理論基礎。
這屬於靜態接觸問題，但是鐵路車輪在軌道上運動屬於滾動接觸問題，其研究比靜態接觸研究複雜。
最“經典”的解決滾動接觸問題的方法可追溯到Carter和Fromm H.。1926年，Carter發表了著名論文“論機車動輪行為”，他將鐵路鋼軌看成彈性半空間，用彈性圓柱體模擬車輪，並將兩者材料常數取為一致，藉助於Hertz理論和彈性半空間理論求解這二位彈性體滾動接觸問題，很巧妙地給出接觸斑中黏著區和滑動區的劃分、作用力的大小和分布以及輪軌之間縱向切向力和蠕滑率的關係定律。他最大的貢獻是他的研究思路和方法為三維彈性體滾動接觸理論研究提供了有效手段。
接觸力學是研究兩個表面接觸的固體相互作用所產生的應力和應變的力學。當兩個接觸體的接觸點產生相對運動並傳遞力和力矩時，就出現有別於靜態接觸的滑動和滾動接觸。鐵道車輪在軌道上運轉時，接觸表面上的質點以滑動和滾動相結合的方式作相對運動。對輪軌滾動接觸及其傳遞牽引力的研究，使滾動接觸理論得以不斷深入和發展。圍繞輪軌滾動接觸問題的求解，研究發展了許多理論模型，統稱輪軌滾動接觸理論。較著名的理論有Carter 理論，Vermeulen-Johnson理論，kalker線性理論，kalker簡化理論，kalker三維精確理論，沈氏理論等。
Hertz接觸理論
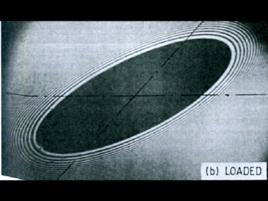
圖1最早對兩個彈性體接觸處應力狀態的令人滿意的分析，是由Hertz在1882年首先做出的，當時他正在研究兩個圓柱透鏡之間間隙中的Newton光學干涉條紋，他注意到由於透鏡之間的接觸壓力對透鏡表面彈性變形可能造成的影響。Hertz發現兩個半徑為R，軸線交角為45°的圓柱透鏡在未載入的情況下，它們之間的干涉條紋顯示出橢圓形等值線特徵，如圖 1所示。從載入條件下的光學干涉條紋圖2不難想像接觸面保持橢圓型區域，於是提出了接觸壓力呈橢圓形分布的假設。
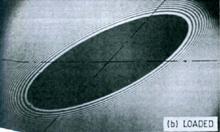圖2Hertz用彈性力學理論研究兩個彈性體的接觸問題，提出了彈性接觸的Hertz理論。Hertz理論中引入了以下假設：(1)表面外形函式以及它的一階和二階導數在接觸區都是連續的，並且是非協調的；(2)小應變；(3)接觸區域的有效尺寸比起每個物體的尺寸和接觸表面的相對曲率半徑是很小的，因此每個接觸物體可被看作是一個半空間；(4)表面無摩擦的，兩個表面之間只傳遞法向壓力。
Hertz接觸理論是建立在無摩擦的彈性接觸面上，所以，它只能對輪軌接觸的法向力進行計算。但由於其形式簡單和使用方便，許多研究人員仍使用它進行輪軌接觸問題的計算。
Carter和Fromm的二維彈性接觸理論
該理論基於Hertz接觸條件，即接觸表面是光滑的、車輪和軌道看成是彈性半空間，接觸斑是平表面的；輪軌接觸點及附近的曲率半徑看作常數，接觸斑的形狀是橢圓，正壓力是半橢球狀。
英國學者F. W. Carter於1926年發表論文《論機車動輪的行為》，研究帶有摩擦的二維滾動接觸理論。輪軌間接觸橢圓的形狀在很大程度上取決於車輪的磨耗程度和軌頭的形狀，並符合按Hertz理論所求的接觸斑橢圓的變化規律。新輪、新軌相接觸時，其接觸橢圓沿縱向的半軸通常大於沿橫向的半軸。然而，當輪軌在運用中磨耗後，其接觸橢圓與上述比對，相當於轉過90°，即縱向半軸小於橫向半軸，可將它近似成二維的長方形條帶。因此，Carter在研究時就假定車輪為一圓柱體，而鋼軌為一半徑無限大的圓柱，則將輪和鋼軌的關係看成圓柱在無限半空間彈性體表面上的滾動，並將兩者的彈性常數取為一致。建立邊界條件後，Carter用半空間逼近圓柱體，並求解兩個半空間接觸的二維彈性（平面應變）問題。Fromm考慮的是兩個具有相同彈性常數的圓柱體的滾動接觸問題，並且在不用半空間近似的情況下，成功地求解這個二維彈性問題。
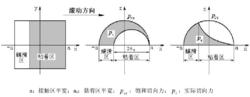圖3 Carter 對黏滑區的劃分及切向應力分布Carter和Fromm都假設接觸力中的切向摩擦力滿足Coulomb摩擦定律，並且均將法向應力分布取為Hertz分布，它們還假設整個接觸區域上有滑動，且方向相同。兩位作者都假設：接觸區分為兩部分，即鄰接前沿的區域，滑動為零的黏著區；和其他鄰接後沿的區域，有滑動的滑動區。Carter對接觸區域的劃分如圖 3所示。
Carter的滾動接觸理論模型雖然只能解決二維接觸問題，但非常實用，至今仍為鐵路工程技術人員使用，他的研究最大貢獻是他的研究方法和思路為後來的學者（Johnson、Kalker等）進行三維彈性體滾動接觸理論研究提供有效手段。其缺點是它不能處理自旋蠕滑，也不能得到三維情形下的無自旋解。
Kalker簡化理論
該理論基於Hertz接觸條件，即接觸表面是光滑的、車輪和軌道看成是彈性半空間，接觸斑是平表面的；輪軌接觸點及附近的曲率半徑看作常數，接觸斑的形狀是橢圓，正壓力是半橢球狀。
在輪軌蠕滑理論研究方面作出很大貢獻的是荷蘭學者Kalker教授。他於1967年在他的博士論文中，用級數方法討論了具有橢圓形接觸區的三維滾動接觸問題，研究中考慮了縱橫向蠕滑率和自旋蠕滑率對接觸斑蠕滑力的影響。
對於準同一Hertz穩態滾動接觸問題，這裡準同一是指兩個接觸體具有相同的材料常數，在受碾壓過程中，可以忽略接觸斑切向力分布對法向位移差的影響，也可以忽略正壓力分布對切向變形的影響。Kalker在研究中假設輪軌接觸區域為全黏著狀態，切向力以及由它得出的合力和旋轉力矩都是蠕滑率和自旋蠕滑率的線性函式，這也是它被稱為Kalker線性蠕滑理論的原因。
1973年，Kalker藉助於線性理論模型法發展了一種快速計算模型－簡化理論。該理論假設彈性體與堅硬地基相固結為一薄層，在接觸區中任意一點彈性位移僅和作用在該點力有關，且某方向的位移僅和其同方向的力有關。該理論的特點是在理論上比較簡單，其配套程式FASTSIM計算速度快，因此適用於車輛運動的分析，是深受車輛動力學研究人員歡迎的輪軌力模型之一。但其計算誤差因條件而異，最大可能達到15%左右 。
