定義
流體靜力學的基本概念之一。指某時刻處處與渦量相切的曲線。如果dl是渦線上的微元向量,Ω是渦量,則確定渦線的微分方程是Ω×dl=0。通過非渦線且不自交的封閉曲線各點的所有渦線所組成的管狀曲面稱為渦管。渦管某截面A上的渦通量為:
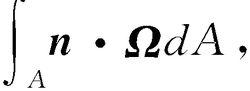 渦線
渦線n是截面A的單位法向量,其方向沿此截面上渦量所指的方向.此渦通量稱為渦管強度。由於渦量Ω的散度一定等於零,渦管強度沿渦管是不變的。渦管不能在流體內部中斷。對真實流體來說,渦管也不能起迄於靜止的固體邊界。
解釋
在連續力學中,渦度是描述在某點附近的連續體的局部旋轉運動(某物旋轉的趨勢)的假動力場,如位於該點的觀察者所看到的,並伴隨著流動。
在概念上,渦度可以通過將所述連線點的一部分標記在所討論的點的小鄰域中,並且當它們沿流動移動時觀察它們的相對位移來確定。渦度矢量將是這些粒子相對於其質心的平均角速度矢量的兩倍,其根據右手規則定向。這個數量不能與顆粒相對於某個其他點的角速度相混淆。
更準確地說,渦度是一個假動子場ω→,定義為流速u→矢量的捲曲(旋轉)。二維流的渦度總是垂直於流的平面,因此可以被認為是標量場。
渦度與(經典)斯托克斯定理沿著封閉路徑的流動循環(速度的線積分)有關。也就是說,對於正常方向n→和面積dA的任何無窮小的表面元素C,沿著C周邊的循環dΓ是點積ω→∙(dA n→),其中ω→是C中心的渦度。
許多現象,例如通過空氣吹出蠟燭,更容易解釋為渦度而不是壓力和速度的基本概念。這尤其適用於渦環的形成和運動。
實例
在像剛體一樣旋轉的連續質量中,渦度是該旋轉角速度矢量的兩倍。例如,在恆定速度下已經圍繞其垂直軸旋轉一段時間的罐中的水的情況。
即使所有顆粒沿著直線和平行的路線流動,如果存在剪下(即,如果流速在流線上變化),則渦度可能非零。例如,在具有恆定橫截面的管內的層流中,所有顆粒平行於管的軸線行進;但在該軸附近更快,並且幾乎固定在牆壁旁邊。渦度在軸上為零,最大值為最大值。
相反,即使流過的顆粒沿著彎曲的軌跡行進,流動也可以具有零渦度。一個例子是理想的非旋轉渦流,其中大多數顆粒圍繞一些直軸旋轉,速度與其與該軸的距離成反比。沒有跨越軸線的一小塊連續體將以某種方式旋轉,但是以相反的方式剪下,使得它們的平均角速度圍繞它們的質心是零。
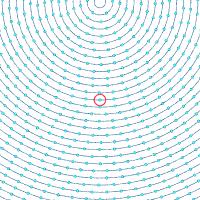 渦線
渦線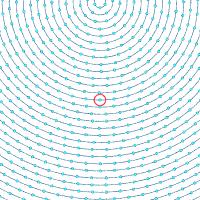 渦線
渦線 渦線
渦線演化
渦度場的演化由渦度方程描述,可以從Navier-Stokes方程得到。
在許多實際流動中,可以忽略粘度(更確切地說,在具有高雷諾數的流體中),渦度場可以通過離散渦流的集合很好地建模,除了在軸周圍的空間的小區域之外,渦度可忽略不計的渦流。在2-D電勢流(即2-D零粘度流)的情況下,這是明顯的,在這種情況下,流場可以被建模為複平面上的復值場。
渦度是理解如何擾動理想潛在流量解決方案來模擬實際流量的有用工具。通常,粘度的存在導致渦旋擴散從渦流核心擴散到通常的流場中。該流量由渦度傳遞方程中的擴散項來解釋。因此,在非常粘稠的流動(例如Couette Flow)的情況下,渦流將在整個流場中擴散,並且比在渦度處觀察速度場可能更簡單。
實際套用
航空
在空氣動力學中,有限翼上的升力分布可以通過假設翼的每個段在其後面具有半無窮遠的後渦。然後可以使用通過翼的表面沒有引起的流動的標準來求解渦流的強度。該過程稱為計算流體動力學的渦流面板方法。然後將渦流的強度相加,以找到關於機翼的總體近似流通。根據Kutta-Joukowski定理,電梯是循環,空速和空氣密度的乘積。
大氣科學
相對渦度是空氣速度場相對於地球的渦度。這通常被建模為平行於地面的二維流,使得相對渦度向量通常垂直於地面,並且然後可以被視為標量,當矢量向上指向時為正,當它向下指向負時。因此,當風逆時針旋轉(俯視地球表面)時,渦度是正的。在北半球,正渦度稱為旋風旋轉,負渦度是反氣旋旋轉;在南半球的命名是相反的。
從相對於慣性框架的空氣流速計算絕對渦度,因此包括由於地球旋轉而產生的科羅利斯參數。
潛在渦度是絕對渦度除以恆定熵(或潛在溫度)水平之間的垂直間距。如果空氣品質在z方向上被拉伸(或壓縮),空氣品質的絕對渦度將改變,但是在大氣中占主導地位的絕熱流中,潛在的渦度是保守的。因此,潛在的渦度因此可用作空氣品質在幾天的時間尺度上的近似示蹤劑,特別是當在恆定熵水平下觀察時。