簡介
海水的密度、溫度、鹽度等熱力學狀態參數隨深度分布的層次結構,通常尤指鉛直尺度不小於常規海洋學觀測層次間距的層次結構。
海洋是處於鏇轉地球上受重力作用的廣袤的含鹽水體。在海面受太陽輻射的不均勻加熱,以及不同氣候帶的大氣的動力學和熱力學作用下,各海區海水的溫度、鹽度和密度都有顯著的差異,但其鉛直分布卻呈現出某種有規律的巨觀層次結構。觀測表明,被太陽輻射加熱的海洋上層,溫度較高,密度較小,導致海水的溫度隨深度而下降,密度隨深度而增加的特性;而重力的作用,則使狀態參數具有這種分布的海水,處於流體靜力學平衡的穩定狀態。在海洋的表層,由於風和波浪的攪拌作用,形成了一個基本均質的水層,其厚度僅約100米。這一水層,通常稱為風混合層或上混合層。在此水層之下,則有一個厚約1000~1500米的過渡層,其中溫度、鹽度和密度隨深度的分布,一般不是漸變的,而是具有一個很大的階躍,有時呈現為一系列的階躍。這樣的水層,通常稱為躍層,或更確切地分別稱為溫度躍層、鹽度躍層和密度躍層。在躍層之下更深的水層中,溫度、鹽度和密度的鉛直分布,幾乎處於均勻狀態。這一水層,稱為深層或下均勻層。
度量海水層結的一個最常用的特徵參數是浮力頻率N(z),即在穩定層結的流體中,受擾動的流體在浮力作用下,相對於平衡位置作上下振盪的固有頻率。
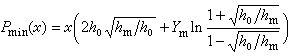
式中g為重力加速度;ρ為海水密度;z為鉛直坐標,原點和海面重合,以向上為正;(dρ/dz)A表示海水作垂直位移的絕熱密度梯度。當N2(z)>0,即(dρ/dz)<(dρ/dz)A時,層結是穩定的;當N2(z)=0,即(dρ/dz)=(dρ/dz)A時,層結是中性穩定的;當N2(z)<0,即(dρ/dz)>(dρ/dz)A時,層結是不穩定的。
在海洋學上,通常還引入若干便於計算的 N2(z)的表達式。例如,按聲速的定義和流體靜力學平衡條件dp/dz=-gρ(p表示壓強),有 (dρ/dz)A=(дρ/дp)A(dρ/dz)=-gρ/c2
式中c表示海水中的聲速。準此,在海洋的上層和中層,除了密度近似均勻的上混合層以外,上式右方的第一項遠大於第二項,而穩定層結條件便簡化為dρ/dz<0。 其次,利用海水狀態方程ρ=ρ(T,p,S)可以導出 式中T為溫度;S為鹽度;cp和cV分別表示海水的定壓比熱容和定容比熱容。對於溫度和鹽度的鉛直梯度都很小的上混合層和深度大於3000~3500米的深層來說,按上式計算N2(z)是很方便的。反之,對於dT/dz和dS/dz較大的水層來說,上式第2項可以忽略不計,於是式中σt=【ρ(T,pa,S)-1】×103為海水的條件密度,pa表示一個大氣壓。
此外,如引入海水的絕熱溫度梯度Γ,則可將N2(z)表示為
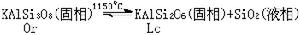
式中α=-(1/ρ)(дρ/дT)p,s,即海水在壓力為p,鹽度為S時的熱脹係數,對於海水來說,一般地有gρΓ埄10-4°C/m,並且α>0。故當鹽度梯度不很大時,層結穩定性條件實際上便歸結為dT/dz>0。
觀測結果表明,在海洋上混合層和深層,N 值最小,其量級為10-3~10-4秒-1(相應的周期為1.7~17小時);在躍層處,N值最大,其量級為10-2秒-1(相應的周期約為10分鐘)。據G.加勒特和W.H.蒙克在1972年發表的研究結果,在大洋中,除了高緯度海區、赤道海區和西部邊界流海區外,上混合層以下的N(z)分布可表示為
N(z)=N(-200)exp【(z +200)/1300】,z ≤-200m
式中N(-200)一般可取為5.23×10-3秒-1。
海水穩定層結的一個重要後果是抑制鉛直方向的運動,而這個約束卻有助於發展準水平的大尺度運動。由於海洋中的大尺度運動是顯著地受地球自轉影響的,因此在穩定層結海洋中大尺度的流速場和密度場之間,存在著密切的關係,這種關係就是海流動力學計算中的“地轉關係”。
海水密度穩定層結的上述效應,通常採用下列兩個無量綱數來度量:
理查孫數
Ri=N2/(дu/дz)2
式中u表示水平流速,有關穩定層結流體中的剪流穩定性的實驗表明,當Ri>1/4時,浮力效應足以抑制由流速鉛直梯度所造成的動力學不穩定性;反之,當Ri≤1/4時,將出現剪下不穩定性,使鉛直方向上的運動和湍流得以發展。對於海洋中的大尺度運動來說,除了近乎均勻的上混合層和近底摩擦層以外,Ri的數值一般介於 104~105之間,因此,可以認為海洋中的大尺度運動總是重力穩定的。伯格數