正文
1958年就已確定，正像電磁相互作用可以用電磁流描寫一樣，弱相互作用可以用弱流描寫。這些流在洛倫茲變換下的性質可以分為矢量流及在空間反射變換下性質相反的軸矢量流兩種類型。60年代初，確定了強相互作用具有近似的 SU(3)對稱性，矢量流及軸矢量流屬於SU(3)的八重表示,流代數是在這些成果的基礎上提出來的，它以這些矢量流及軸矢量流算符在同一時刻的對易關係(等時對易關係)形成的代數結構作為基本假設。此外，在具體套用流代數時，還常常假設矢量流守恆及軸矢量流部分守恆,後者原來是對SU(2)的軸矢量流提出的，其確切含意是同位鏇軸矢量流的散度正比於 h介子質量的二次方與h介子場算符的乘積。由於h介子的質量很小，這一假設意味著同位鏇軸矢流近似地守恆，所以稱為部分守恆。有時也把這一假說推廣到SU(3)的軸矢量流。此時將由相應的贗標介子代替 h介子。由於其他贗標介子的質量比h介子的大得多，所以,對於推廣出來的那些軸矢量流，部分守恆假設的準確程度會比同位鏇軸矢量流差得多。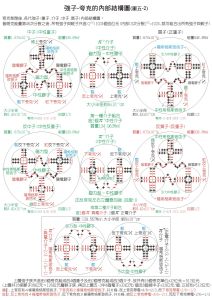
強子-結構模型圖流代數與強子結構模型是密切相關的。原則上，如果強子的組分及其動力學研究清楚了，就可以導出流代數。但是在60年代中期，強作用的理論還沒有建立（即使到現在，儘管強作用理論取得了很大的進展，也仍有大量問題沒有得到解決），所以流代數的做法是不管強作用的具體形式，直接從對流的代數結構的假設出發。最常用的流代數的具體結構假設為與自由夸克模型中流算符滿足的代數一樣。具體地研究存在相互作用時的夸克模型流對易子，發現確實只有少數很少套用的對易子（涉及流算符的空間分量的）與相互作用有關。
最早套用的流代數是所謂荷代數。荷算符是流算符的時間分量在給定時刻對全空間的積分。1965年,假設荷算符滿足SU(3)×SU(3)李代數，並套用軸矢量流部分守恆假設，導出了阿德勒－韋斯伯格(Adler-Weisberger)求和規則，把核子的軸矢量流耦合常數gA與矢量流耦合常數gv 的比值與h介子－核子總截面聯繫起來,與實驗符合得很好。對於超子的弱耦合常數，得到的結果也大體上與實驗符合。所以，普遍認為，荷代數已經得到實驗的證實。
只考慮流算符時間分量(但不對全空間積分)的時間分量代數與矢量流守恆假設一起導致卡比玻－拉迪卡蒂(Cabbibo-Radicati)求和規則以及德雷爾-赫恩(Drell-Hearn)求和規則（後一規則也可由其他理論導出），前者把核子電磁形狀因子與光生截面聯繫起來，後者把質子的反常磁矩與自鏇平行及反平行於質子自鏇的光子被質子吸收的截面聯繫起來。把實驗數據用模型處理後與之比較，結果也符合。不過這些檢驗是依賴於數據處理的模型的。
涉及流的空間分量的代數的研究及套用均很少。
套用部分軸矢量流守恆假設以及將 h介子質量從物理值延拓到零時矩陣元緩慢變化的假設，導致了有關輻射及吸收低能h介子的低能定理。它與流代數一起,已套用於s波h介子－核子散射長度的計算及一些半輕子和非輕子衰變過程。
60年代末到70年代初，隨著高能量實驗的發展，提出了光錐流代數。其特點是用光錐間隔的流對易子假設代替流的等時對易子假設。很快就發現，光錐流代數與樸素的部分子模型等效。由於部分子模型給出了更清晰的物理圖像，並且，在部分子模型的基礎上，用微擾量子色動力學計算高階輻射修正，預言了實驗上現已看到的標度無關性的微小破壞，所以，光錐流代數的研究已經停滯了。
