概念
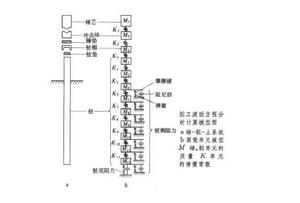
波動方程就是描述波動現象的偏微分方程。打樁時，錘擊能量克服土對樁的阻力而把樁擊入土中。對於直徑大、長度長的樁，按慣用的動力打樁公式預測樁的承載力等問題已不能適應。其原因是，它們把打樁過程看成是兩個絕對剛體自由碰撞問題，認為錘擊能量瞬間就傳遞到樁底，但實際上打樁的能量是以一種應力波的方式向下傳遞，所以用波動方程能給打樁提供較合理的分析。
波動方程有限差分正演模擬誤差來源分析
波動方程有限差分模擬方法是波場數值模擬中最為流行的方法之一，但在用有限差分方法求解波動方程時，常常會產生不期望的數值頻散或稱格線頻散，導致數值模擬結果解析度的降低。所謂數值頻散實質上是一種因離散化求解波動方程而產生的偽波動，它是有限差分方法求解波動方程時所固有的本質特徵，無法避免，但是可以通過合適的參數選擇和適當的數學方法予以減小。
在做有限差分波動方程正演數值模擬時主要是要綜合考慮差分格式、震源的選擇、邊界條件的處理等問題。這些問題能否正確處理直接影響正演模擬結果的正確性，並且誤差是由這些因素綜合影響，如果其中任何一個問題得不到恰當地處理，都會給正演結果帶來誤差。
高階有限差分法在做波動方程正演模擬時，具有計算速度快、頻散較小的特徵，在做有限差分正演過程中必須注意震源、邊界條件等因素的影響，否則就會出現意想不到的結果。總體來說選擇較小的空間和時間步長能保證結果的正確性，但是時間和空間的步長的減小必定增加運算的時間，因此要保證運算速度與精度就必須處理好各個參數之間的關係。
波動方程分析法在動力驗樁中的套用
長期以來，建築工程界廣泛使用動力打樁公式來確定樁的靜承載力。由於打樁公式是從能量守恆原理以及自由體的碰撞原理推導出來的，未考慮應力波在樁身中傳播的過程，因而有較多的經驗的成分。1960年，Smith EAL第1次將描述波在桿中傳播的波動方程的數值解方法套用於實際的打樁分析中，但 Smith 法的主要缺點是缺少土的特性描述。1964年，美國的Case技術學院開始對樁基應力波檢測進行系統的、大規模的研究，1975年，他們提出了兩種波動方程分析方法，即Case法和CAPWAP法。從此，利用波動方程分析方法進行動力驗樁得到了不斷發展。
Smith法
Smith法是將錘、墊層、樁帽和樁以及樁周土看作一個系統，並用質量- 彈簧系統來表示。無論對樁尖土阻力或樁周土阻力，Smith法均採用粘彈塑性數學模型來描述。在土的變形過程中，首先是發生彈性變形，其最大彈性位移用q表示。在位移超過q時，土將產生塑性流動，其應力保持不變，稱為極限應力或阻力Ru。對於土的動阻力 Rd，假設服從牛頓粘滯定律，其阻力與質點速度成正比。
CAPWAP法
Case法和CAPWAP法這兩種方法的基本原理是一致的，即以重錘在樁頂衝擊產生一個足夠強的應力波沿樁身向下傳播。在這個過程中，波所通過的部分，樁身經受了較高的壓縮變形，產生了較大的向下質點位移，因而產生了一個瞬變的摩擦力。由於這個摩擦力是瞬變的力，它將在樁身中和樁周土中各激發出兩個波。樁本身是一個波導體，在樁身中所激發出的兩個波，一個是沿樁身向上傳播的壓縮波，它到達樁頂時被感測器記錄下來；另一個是沿樁身向下傳播的拉伸波，經樁底反射後也返回樁頂，其回響也被感測器記錄下來。隨著波陣面的不斷向下運動，所產生的摩阻力信息也不斷地通過這些波沿樁身傳向樁頂。這樣一來，摩阻力沿樁身的變化就直接反映到了樁頂波回響隨時間的變化中。
研究結論
利用波動方程分析方法進行動力驗樁開始增多，這種方法在準確的土信息的基礎上預測打樁過程，計算樁的承載力，克服了長期以來使用動力打樁公式確定樁的承載力時所具有的較多的經驗成分。
Smith法的主要缺點是缺少土的特性描述。Case法和CAPWAP法雖然解決了這一問題，但其自身也有一些缺點。在CAPWAP法的計算中，每一次疊代都需要修正相對應的所有樁單元的樁周土的土性參數，並重新求解波動方程。如果樁單元較多(每個樁單元相對應 3個土性參數)，幾十個土性參數同時調整是非常困難的，需要一定的經驗和相當的技術知識基礎。同時，CAPWAP法多次的求解過程也需要花費很多的時間。Case法是一個簡化的分析方法，它建立在許多的假定的基礎上，因而所得結果的誤差較大。
時柵的波動方程分析與行波形成新方法
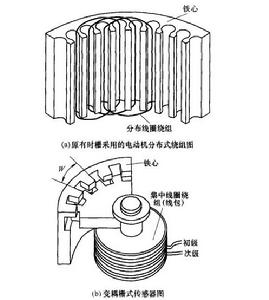圖1 基於變禍變壓器原理的柵式感測器原理圖(局部)時柵經多年研究己取得重要突破。在產品化過程中逐漸凸現的問題是 ：以往採用的旋轉磁場是基於傳統交流電動機的定子繞組而得到的。電動機作為動力裝置，對繞組均分性要求不高，而時柵雖然比光柵的加工精度要求低得多，但作為精密檢測元件仍然具有一定的精度指標。此外，從原理上說，除了“旋轉磁場切割金屬導體”的方法以外，還有沒有別的行波形成方法? 為此需進一步對時柵的波動方程進行分析，探索新的行波形成方法，以加深對“時空轉換”的認識並進一步降低對精密機械加工的依賴和成本。
新方案的優勢及啟示
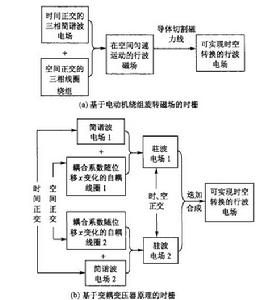圖2 兩種時柵的行波電場產生原理框圖在弄清楚了最終需要的是能實現時空轉換的電行波以及電行波的形成機理後 ，就尋求一種儘可能簡便的電行波形成方式，這裡提出一種利用式AsinαBcosβ+ AcosαBsinβ=ABsin（α+β）=Ksin（α+β）直接形成電行波的方法。當α為時間自變數，β為空間自變數，上式就是一個典型的行波表達式。
上述方案可以很好地解決前述時柵產品化過程存在的問題。
（1）時柵的原始機械精度不再依賴線圈分布的均勻性即等分精度，轉而依賴齒的等分精度，而依靠一般的線切割或切齒加工或澆鑄加工都可以保證圖1端面齒的等分精度。換言之，圖1所示分布線圈是一圈圈零散的線束，精度很難控制，而集中線圈加分齒的精度則容易保證。
（2） 圖1b所示的集中線包繞制比圖1a的分布線圈繞制簡單得多，工藝大大簡化，成本更低。
（3）此方案的研究思想已跳出電動機繞組旋轉磁場的思路，而利用駐波電場直接合成行波電場，這為獲取行波電場開闢了一條新路。兩種方式在原理上的區別如圖2所示。
研究結論
（1）通過對場式時柵波動方程的分析，尤其是對電行波和磁行波的分析，可以得到一個全新的重要結論：磁行波和電行波雖然數學表達式完全相同，其物理意義卻截然不同。前者是在空間軸上的前進和後移，後者是在時間軸上的超前和滯後。據此結論，可以加深對時空坐標轉換方法、信號產生機理的認識，進而構思出更加巧妙合理和更新穎的感測器結構形式。
（2）根據上述研究，明確時空轉換的最終目的是要得到一個電行波(時間行波)。於是提出了一種不同於旋轉磁場方法，而用變禍合變壓器原理的兩路駐波來直接合成電行波的新方法。研究思路進一步打開，設計的時柵結構形式更簡單合理，有利於加速成果的產品化進程。
