氣體分子的平均自由程

氣體分子的平均自由程

正文

氣體分子相繼兩次碰撞間所走路程的平均值。在氣體分子的碰撞理論的剛球模型中，認為分子只在碰撞的一剎那發生相互作用，而在其他時間內，分子作直線運動。相繼兩次碰撞間所走的路程叫分子的自由程。由於氣體分子的數目很大，碰撞頻繁，運動的變化劇烈，故其自由程只有統計意義。以速率v運動的分子,在dt時間內走過υdt的路程，受到碰撞的可幾次數是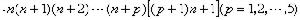dt,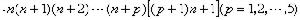是碰撞頻率。一個分子相繼兩次碰撞的時間為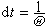。自由程l(υ)為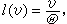

由此得到的自由程與分子的速度有關，對各種速度求平均，就得到平均自由程。用平衡態的麥克斯韋分布求出的平均自由程有兩種。
① 麥克斯韋平均自由程 l。規定為氣體分子的平均速度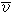與平均碰撞頻率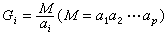之比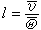。如此得到的平均自由程為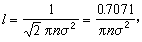

式中n為分子的數密度，σ為分子的半徑。
② 泰特平均自由程lT。規定為氣體分子的速度與碰撞頻率之比的平均為lT＝<v/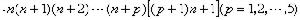>。如此算得的平均自由程為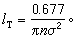

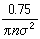1857年還未發現氣體分子的速度分布律，R.克勞修斯假定氣體分子的速率相同而方向不同，最先引入了自由程的概念。克勞修斯的自由程lC為。
通常所說的平均自由程是麥克斯韋平均自由程。利用理想氣體狀態方程P＝nnt，可將平均自由程的公式換成溫度T 和壓強P的函式

式中n是玻耳茲曼常數。
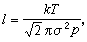
標準狀態下，空氣分子的有效直徑為 3.5×10-10m，平均分子量為29，利用上述公式算出其平均自由程為l=6.9×10-8m。可見,在標準狀態下，空氣分子的平均自由程約為其有效直徑的200倍。

氣體分子的平均自由程

在氣體輸運的初級理論和真空技術、氣體放電等領域中，平均自由程都是常用的重要物理量。

配圖

相關連線