氣體分子的碰撞

只當第二分子的中心落在虛球上才發生碰撞。 氣體分子的碰撞 氣體分子的碰撞力心點模型

氣體分子的碰撞

正文

氣體分子相互作用的一種基本過程。碰撞改變了氣體分子的速度，大量分子頻繁的相互碰撞，影響了氣體的輸運過程(見氣體的輸運現象)。在氣體動力論中，不考慮分子的內部結構，不考慮平動以外的各種運動形式，因此一切碰撞都是彈性碰撞，碰撞前後動量及能量的總和都保持不變。因為三個以上分子同時碰撞的機會很少，在研究氣體分子的碰撞時，只考慮主要的二體碰撞過程。在二體碰撞中,以n表示碰撞時刻由第一分子(質量為m1)的中心到第二分子（質量為m2）中心方向上的單位矢量，以g12 表示碰撞前二分子的相對速度g12＝v1-v2,根據能量守恆和動量守恆定律，可以得到碰撞後二分子的速度分別為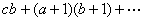

分子的碰撞機構很複雜，常用兩種分子模型來簡化其理論處理：一個是剛球模型，另一個是力心點模型。
剛球模型　認為氣體分子是剛性球，碰撞時球的大小和形狀都不改變，並且球面是光滑的，在碰撞的一剎那，接觸面沒有影響切面方向相對運動的摩擦阻力。以θ表示n與F12之間的夾角,只有在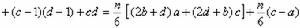時才能發生碰撞。以σ1、σ2分別表示兩彈性剛球的直徑，以第一分子的中心為球心，以為半徑作一虛球如圖1所示。只當第二分子的中心落在虛球上才發生碰撞。在計算碰撞頻率時，L.玻耳茲曼引進了分子混沌性假設：不論第一種分子的速度如何，都不影響它附近第二種分子的速度分布函式。因而算出一個速度為v1的分子，在單位時間內與速度為v2、位於速度間隔dv2內的第二種分子的碰撞數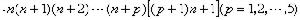12為

式中f2為第二種分子的速度分布函式。在平衡態時, f2是麥克斯韋分布（見麥克斯韋速度分布律）。因而一個第一種分子與第二種分子的平均碰撞數為

式中n2是第二種分子的數密度,n是玻耳茲曼常數。當只有一種分子時，則單位時間內一個分子的平均碰撞數為

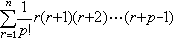
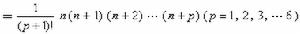
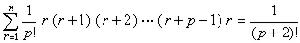
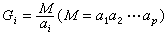式中 n為分子的數密度。標準狀態下氧分子的平均碰撞數是＝6.65×109秒-1。

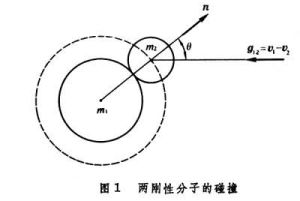氣體分子的碰撞

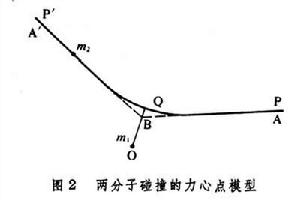氣體分子的碰撞

力心點模型　把分子看作是質點，分子間相互作用力是中心力（見輳力場），相互作用能只是分子間距離的函式。以圖2表示碰撞過程。O 點為第一分子的中心，PQP‵為第二分子中心相對於第一分子中心所走的軌道，ABA‵為軌道PQP‵的漸近線，OBQ在一條直線上，OQ 為兩分子相距最近的距離。當第二分子走到 Q點時就認為發生了碰撞。由於相互作用勢Φ(r)具有各種形式,力心點模型的碰撞頻率計算很複雜。只在特殊作用能Φ(r)=nr-s（式中 n、s是兩個常數）情況下可以得到一定的結果。
氣體輸運過程的初級理論主要是從分子相互碰撞的情況去研究各個具體的輸運過程；在輸運的數學理論中也要考慮碰撞的影響。剛球模型的計算簡單，對許多實際問題可以提供一些初步理論，其缺點是與實際氣體分子的性質相差較大，計算結果與實際情況符合較差；力心點模型與實際分子的性質較為接近，但計算複雜，且實際分子都有內部結構，只當氣體分子相距較遠時，才能把它們當作質點看待。所以當氣體密度不太高時，用該模型計算的結果與實際情況較符合；而當氣體密度很高時，用該模型計算的結果與實際情況差異就較大了。

配圖

相關連線