正常著色

正常著色是一種組合方法，指對一個集合中元素的一種著色方法。設有一個集合A，在A的元素間有一種二元關係R，若將A中的元素著以顏色使得A中任何兩個滿足R的元素均帶不同的顏色，則這種著色方法為A對於R的正常著色。若A為一個圖G的節點集，這二元關係R就是相鄰，則稱這種著色為G的點正常著色，通常簡稱正常著色或著色；若一種著色中所用顏色的數目為k，則稱這種正常著色為k點正常著色；若取A為圖G的邊集，R為邊之間的相鄰,則這種正常著色稱為G的邊正常著色，常簡稱邊著色；若圖G的一種邊正常著色共用k種不同的顏色，則稱它為G的k邊正常著色；對於一個圖的某種點正常著色，著相同色的節點所組成的集合稱為一個色組，對於一平面圖或曲面上的地圖的面集，面的相鄰關係的正常著色，通常簡稱面著色，若一個面正常著色中共用k種顏色，則稱它為k面正常著色，也稱為k面著色。所謂全正常著色，就是對於一個圖的節點集和邊集的並在相鄰(當兩元素同為節點或同為邊時)或關聯(當一個元素為節點另一個為邊時)關係下的正常著色，全正常著色常簡稱全著色。

定義

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

圖的 正常著色(簡稱 著色)一般是指對它的每一個結點指定一種顏色，使得沒有兩個鄰接的結點有同一種顏色。如果圖著色時用了種顏色，則稱圖為- 可著色的，對於圖著色時，需要的最少顏色數稱為 著色數，記作。

相關性質定理

定理1 任意 平面圖最多是5-可著色的。

定理2 ( 四色定理)任何平面圖都是4一可著色的。

正常著色

正常著色

定理3 若是 簡單圖，則。

正常著色

證明: 對的階數n進行歸納。

正常著色

正常著色

正常著色

當 時， ，這時△=0， ，結論成立。

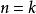正常著色

正常著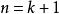色

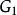正常著色

正常著色

正常著色

正常著色

正常著色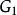

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

正常著色

設時結論成立。考慮 時的情形，任取G中一個結點 。令 ，則 是k階簡單圖，由歸納假設 ，另一方面 ，於是有 ；設在G中 的鄰接點是 ，則 ，因此，用 種顏色對 正常點著色時， 最多只能用其中的 種顏色，即至少可以剩下一種顏色用於 的著色，這就是說 。

正常著色

正常著色

正常著色

當是完全圖和奇圈時，定理中等號成立，Brooks進一步證明過，對於既不是完全圖也不是奇圈圖的簡單連通圖，不等號嚴格成立，即在這種情況下有 。

決定一個圖的色數不是一件容易做的工作，事實上人們還未找到一個普遍有效的方法，但是也有一些很好的近似方法可以利用。

著色方法

韋爾奇·鮑威爾法

正常著色

用韋爾奇 ·鮑威爾法可以用最少的顏色數對任意圖進行正常著色，該方法的步驟如下：

正常著色

(1)將圖中的頂點按度數遞減的次序進行排列（如果有相同度數的頂點，這種排列是不唯一的）；

(2)用一種與已著色頂點所有顏色不同的新的顏色C對排列最靠前的尚未著色的頂點著色，並按排列次序對與前面已著上顏色C的頂點不鄰接的每一頂點著同樣的顏色C；

(3)反覆重複步驟(2)，直到所有頂點全部著上顏色為止；

整個過程所用的顏色數即為該圖的色數。

獨立集分劃法

正常著色

正常著色

定理 令 是色數為的圖，則存在下述著色方式：

正常著色

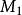正常著色

(1)著第一種顏色的結點構成的一個極大獨立集 ；

正常著色

正常著色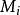

正常著色

正常著色

(2)對每個 ，著第 種顏色的結點構成 的極大獨立集 。

根據這個定理。可以構造如下方法：

正常著色

第一步：求出 中全部的極大獨立集；

正常著色

正常著色

第二步：對前面已求得的每個極大獨立集，構造圖 ；

第三步：對第二步中構造的圖找出全部的極大獨立集．冉類似地重複第二步。

顯然，當某一步得到的子圖是個零圖時，這個零圖的結點構成圖的一個獨立集，從原圖得到這個零圖的過程中每次刪去的極大獨立集全體構成了結點集的一個獨立分劃。

上述方法就是找出所有的這種分劃，其中由分塊數最少的分劃給出圖的色數。但是，這種方法的工作量太大，經過改進，人們證明只需在上述方法中把求全部極大獨立集改為求包含圖的最大度結點的全部極大獨立集就行了，儘管如此，求色數的工作量仍是相當可觀的。

舉例分析

正常著色

例1 求圖1所示的圖的色數。

圖1

正常著色

解：用韋爾奇 ·鮑威爾法對 進行著色，整個過程如表1(a)~(d)所示。

表1

(a)		(b)		(c)		(d)
頂點	顏色	頂點	顏色	頂點	顏色	頂點	顏色
b	紅	b	紅	b	紅	b	紅
c	—	c	—	c	黃	c	黃
d	—	d	—	d	—	d	藍
e	—	e	—	e	黃	e	黃
f	—	f	紅	f	紅	f	紅
a	—	a	—	a	—	a	藍
g	—	g	—	g	—	g	藍

正常著色

正常著色

正常著色

正常著色

正常著色

將圖中頂點按照度數由大到小排序，得到序列 ，首先，將頂點b著上紅色，並且將與b不鄰接的頂點 也著上紅色；其次，將頂點c著上黃色，並將與c不鄰接的e也著上黃色；接下來，將頂點d著上藍色，並將與d不鄰接的a也著上藍色，g與d和a均不鄰接，因此它也可以著上藍色，這樣整個著色過程就結束了，的色數 。

例2 考試安排問題，期末每個學校都要舉行考試，設學校開設的課程集合為X，學生集合為Y，要求學同一門課程的學生考試時間儘可能相同，問至少要舉行多少場考試？

正常著色

正常著色

正常著色

正常著色

對於這個問題，可以用一個圖G來描述，結點表示考試課目，結點 和 鄰接當僅當有學生既要參加 課程的考試，又要參加 課程的考試，那么，所得圖的每一種點著色方案都給出了考試的一種安排方式。而最少的考試場次正好對應著找圖的點色數。