簡介
在數論中, 正則素數的概念首先由恩斯特·庫默爾在1847年為了處理費馬最後定理而引入。它具有許多種等價的定義方式。其中之一是:
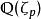 正則素數
正則素數定義:素數p是正則素數,若且唯若p不整除分圓域 的類數。
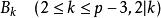 正則素數
正則素數此定義美則美矣,卻不容易計算。另一種定義方式是:素數p是正則素數,若且唯若p不整除伯努利數 的分子。
頭幾個正則素數為:
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, ... (OEIS中的數列A007703)
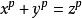 正則素數
正則素數庫默爾證明了:當p是正則素數時, 不存在非零整數解。最小的10個非正則素數是37、59、67、101、103、131、149、157、233、257(OEIS中的數列A000928)。 已知存在無窮多個非正則素數,而迄今仍未知是否存在無窮多個正則素數。
費馬大定理
費馬大定理,也稱 費馬最後定理(法語:Le dernier théorème de Fermat);(英語:Fermat's Last Theorem),其概要為:
當正整數n>2時,關於x,y,z的不定方程
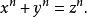 正則素數
正則素數沒有正整數解
以上陳述由17世紀法國數學家費馬提出,一直被稱為“費馬猜想”,直到英國數學家安德魯·懷爾斯(Andrew John Wiles)及其學生理查·泰勒(Richard Taylor)於1995年將他們的證明出版後,才稱為“費馬大定理”。這個猜想最初出現費馬的《頁邊筆記》中。儘管費馬表明他已找到一個精妙的證明而頁邊沒有足夠的空位寫下,但仍然經過數學家們三個多世紀的努力,猜想才變成了定理。在衝擊這個數論世紀難題的過程中,無論是不完全的還是最後完整的證明,都給數學界帶來很大的影響;很多的數學結果、甚至數學分支在這個過程中誕生了,包括代數幾何中的橢圓曲線和模形式,以及伽羅瓦理論和赫克代數等。這也令人懷疑當初費馬是否真的找到了正確證明。而安德魯·懷爾斯由於成功證明此定理,獲得了包括邵逸夫獎在內的數十個獎項。
恩斯特·庫默爾
恩斯特·愛德華·庫默爾(Ernst Eduard Kummer,1810年1月29日-1893年5月14日),德國數學家。庫默爾的研究領域主要有三個方面:函式論、數論和幾何。在函式論方面,他研究了超幾何級數,首次計算了該級數單值群的代入值。在幾何方面,他研究了一般射線系統,並用純代數方法構作了一個四次曲面,它有16個孤立的二重點,16個奇異切平面,現在稱之為庫默爾曲面。庫默爾在數論上花的時間最多,貢獻也最大。最重要的是他提出了理想數的概念。當時庫默爾所關心的問題首先是高斯研究過的高次互反律,其次是費馬大定理。
數論
數論是純粹數學的分支之一,主要研究整數的性質。被譽為“最純”的數學領域。正整數按乘法性質劃分,可以分成質數,合數,1,質數產生了很多一般人也能理解而又懸而未解的問題,如哥德巴赫猜想,孿生質數猜想等,即。很多問題雖然形式上十分初等,事實上卻要用到許多艱深的數學知識。這一領域的研究從某種意義上推動了數學的發展,催生了大量的新思想和新方法。數論除了研究整數及質數外,也研究一些由整數衍生的數(如有理數)或是一些廣義的整數(如代數整數)。
