簡介
歐幾里得幾何是在約公元前300年，由古希臘數學家歐幾里得建立的角和空間中距離之間聯繫的法則。歐幾里得首先開發了處理平面上二維物體的“平面幾何”，他接著分析三維物體的“立體幾何”，所有歐幾里得的公理被編排到幾何原本。
這些數學空間可以被擴展來套用於任何有限維度，而這種空間叫做 n維歐幾里得空間（甚至簡稱n 維空間）或 有限維實內積空間。
這些數學空間還可被擴展到任意維的情形，稱為 實內積空間（不一定完備），希爾伯特空間在高等代數教科書中也被稱為歐幾里得空間。 為了開發更高維的歐幾里得空間，空間的性質必須非常仔細的表達並被擴展到任意維度。 儘管結果的數學非常抽象，它卻捕獲了我們熟悉的歐幾里得空間的根本本質，根本性質是它的平面性。 另外儲存在其他種類的空間，例如球面非歐幾里得空間，相對論所描述的四維時空在重力出現的時候也不是歐幾里得空間。
直覺概述
有一種方法論把歐幾里得平面看作滿足可依據距離和角表達的特定聯繫的點所成的集合。其一是平移，它意味著移動這個平面就使得所有點都以相同方向移動相同距離。其二是關於在這個平面中固定點的旋轉，其中在平面上的所有點關於這個固定點旋轉相同的角度。歐幾里得幾何的一個基本原則是，如果通過一序列的平移和旋轉可以把一個圖形變換成另一個圖形，平面的兩個圖形（也就是子集）應被認為是等價的（全等）。（參見歐幾里得群）。
為了使這些在數學上精確，必須明確定義距離、角、平移和旋轉的概念。標準方式是定義歐幾里得平面為裝備了內積的二維實數的向量空間。有著:
•在這個向量空間中的向量對應於在歐幾里得平面中的點，
•在向量空間中的加法運算對應於平移，
•內積蘊涵了角和距離的概念，它可被用來定義旋轉。
一旦歐幾里得平面用這種語言描述了，擴展它的概念到任意維度就是簡單的事情了。對於大多數部分，辭彙、公式、和計算對更高維的出現不造成任何困難。（但是，旋轉在高維中是非常微妙，而高維空間的可視化仍很困難，即使對有經驗的數學家也一樣）。
歐幾里得空間的最後問題是它在技術上不是向量空間，而是向量空間作用於其上仿射空間。直覺上，區別在於對於原點應當位於這個空間的什麼地方沒有標準選擇，因為它可以到處移動。這種技術本文中很大程度上被忽略了。
歐氏拓撲
歐幾里德平面
歐幾里德平面因為歐氏空間是一個度量空間，因此也是一個具有由度量推導出的自然拓撲的拓撲空間。上的度量拓撲被稱為是歐氏拓撲。歐氏拓撲中的集是開的若且唯若它包含了該集的每一點周邊的開球。可以證明，歐氏拓撲等價於上的積拓撲。
歐幾里德平面 歐幾里德平面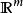 歐幾里德平面
歐幾里德平面 歐幾里德平面關於上拓撲的一個並不淺顯易懂的重要結論是，魯伊茲·布勞威爾的區域不變性。任意的子集（以及其子拓撲）與另外一個的子集同胚的話，那么這個子集自己是開的。這個結果的一個直接的結論就是與不同胚，當。
與流形的關係
在現代數學中，歐幾里得空間形成了其他更加複雜的幾何對象的原型。特別是流形，它是邏輯上同胚於歐幾里得空間的豪斯多夫拓撲空間。
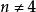歐幾里德平面 歐幾里德平面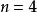
歐幾里德平面n維歐氏空間是n維流形的典型例子，事實上也就是光滑流形。對於，任意與同胚的可微n維流形，也是微分同胚的。值得驚奇的結果是，1982年西蒙·唐納森證明了對於的情況不成立；其反例被稱為是怪 R。
歐幾里德平面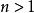
歐幾里德平面歐氏空間也被理解為 線性流形。一個中的m維線性子流形是一個（作為仿射空間）嵌入其中的m維歐氏空間。例如，任意高維（）歐氏空間中的任意直線是該空間中的一個1維線性子流形。
一般的說，流形的概念包含了歐幾里得幾何和非歐幾里得幾何二者。在這個觀點上，歐幾里得空間的根本性質為它是平坦的，也就是非彎曲的。現代物理學特別是相對論，展示我們的宇宙不是真正的歐幾里得時空。儘管這在理論上甚至在某些實際問題如全球定位系統和航空中是重要的，歐幾里得模型仍足夠精確的用於大多數其他實際問題。
相關條目
•歐幾里得幾何
•歐幾里得距離
•閔可夫斯基時空
•黎曼幾何
