淵源
《韓詩外傳》卷二:“夫道二,常之謂經,變之謂權,懷其常道,而挾其變權,乃得為賢。” 宋 葉適 《周純臣子去病淑慧而短折賦以哀之》詩:“其守過老蒼,其行通變權。”
權函式的估計
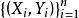 權函式
權函式給定樣本,權函式估計就是條件回歸函式m(x)的估計m^(x),可表示成下述形式:
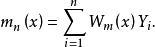 權函式
權函式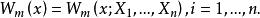 權函式
權函式其中權函式
權數與加權法
統計學認為,在統計中計算平均數等指標時,對各個變數值具有權衡輕重作用的數值就稱為權數. 例子:求下列數串的平均數 3、4、3、3、3、2、4、4、3、3、 一般求法為(3+4+3+3+3+2+4+4+3+3)/10=3.2 加權求法為(6*3+3*4+2)/10=3.2 其中3出現6次,4出現3次,2出現1次.6、3、1就叫權數。這種方法叫加權法。 一般說的平均數,就是把所有的數加起來,再除以這些數的總個數。表示為: (p1+p2+p3+…..+pn)/n; 但有的數據記錄中有一些相同的數據,在計算的時候,那一個數有幾個相同數,就把這個數乘上幾,這個幾,就叫權,加權,就是乘上幾後再加。平均數還是要除以總個數。 還是以上面的各個數為例: 它們每個數都有一些相同數,表示為:k1,k2,k3…….kn; 加權平均的公式是:(k1p1+k2p2+k3p3+……knpn)/(k1+k2+k3+…..kn).
示例
要理解加權是什麼意思,首先需要理解什麼叫“權”,“權”的古代含義為秤砣,就是秤上可以滑動以觀察質量的那個鐵疙瘩。《孟子·梁惠王上》曰:“權,然後知輕重。”就是這意思。
例子:學校算期末成績,期中考試占30%,期末考試占50%,作業占20%,假如某人期中開始得了84,期末92,作業分91,如果是算數平均,那么就是(84+92+91)/3=89;、
加權後的,那么加權處理後就是84*30%+92*50%+91*20%=89.4,這是在已知權重的情況下; 那么未知權重的情況下呢?想知道兩個班的化學加權平均值,一班50人,平均80,二班60人,平均82,算數平均是(80+82)/2=81,加權後是(50*80+60*82)/(50+60)=81.09.還有一種情況類似第一種也是人為規定,比如說你覺得專家的分量比較大,老師其次,學生最低,就某觀點,滿分10分的情況下,專家打8分,老師打6分,學生打7分,但你認為專家權重和老師及學生權重應為0.5:0.3:0.2,那么加權後就是8*0.5+6*0.3+7*0.2=7.2,而算數平均的話就是(8+6+7)/3=7。