概念
模態疊加法又稱“振型疊加法”，它是 以系統無阻尼的振型（模態）為空間基底，通過坐標變換，使原動力方程解耦，求解n個相互獨立的方程獲得模態位移，進而通過疊加各階模態的貢獻求得系統的回響。
實用中，這種方法一般是保留少數振型疊加的截斷形式出現，因此就產生了兩種不同的方法：模態位移法和模態加速度法。
基本原理
無阻尼體系
下面首先通過簡支梁的彎曲振動，說明用振型疊加法求解無阻尼分布參數體系動力反應的原理和做法。
分布參數梁的運動方程為：
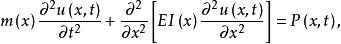模態疊加法
模態疊加法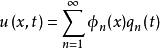將 代入上式，得：
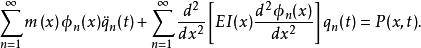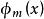模態疊加法
模態疊加法將上式的每一項都乘上 ，並積分，得：
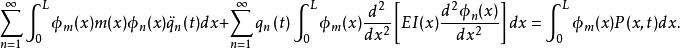模態疊加法
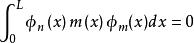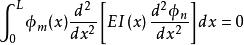模態疊加法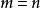
模態疊加法
模態疊加法由正交條件 和 兩個式子，上面的級數中除了 項外，其餘各項都等於零，於是
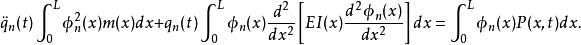模態疊加法
模態疊加法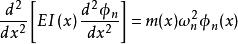將 代入上式，得：
模態疊加法
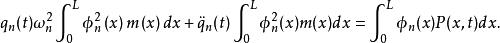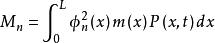模態疊加法
模態疊加法
模態疊加法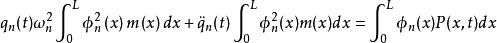 模態疊加法
模態疊加法記 和 分別表示第 階振型質量和對應第 階振型力，則 的式子可簡化為
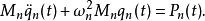模態疊加法有阻尼體系
對於分布參數的有阻尼體系，其運動方程為：
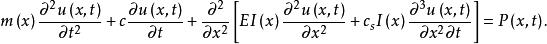模態疊加法 模態疊加法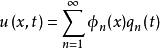將 代入上式，得：
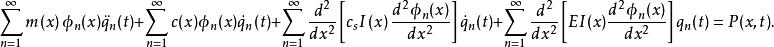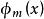模態疊加法 模態疊加法將上式的每一項都乘上 ，積分得：
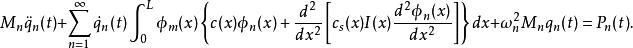模態疊加法顯然，在一般情況下，上式中的阻尼項相互耦聯，因此需要聯立方程組求解。但是，如果假定為經典阻尼，則運動房產中的阻尼項解耦，可以直接將運動方程改寫為：
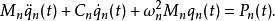模態疊加法可見，體系的總反應等於各個振型貢獻的疊加。與離散多自由度體系相同，對於大多數類型的荷載，分布參數體系各個振型所起的作用一般是頻率最低的振型最大，高振型則趨向減小。因而在疊加過程中通常不需要包含所有的高振型，當動力反應達到精度要求時，即可捨棄級數的其餘各項，從而大大減少了計算工作量。此外，對於複雜結構，其高階振型的數學建模的可靠性相對較小，在動力反應分析時限定要考慮的振型數也是很必要的。
