長時間以來,測定和計算下墊面和近地大氣易之同的動量、熱量和物質傳輸的方法主是依據梯度擴散理論,其原因是這種方法不但具有一定的物理基礎,同時實際套用1時也簡單方便,在算通量時,它只需要某物理屬性的部線分布,而這是比較容易測定的。
原理
梯度擴散的普遍形式可表示為:
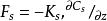 梯度擴散
梯度擴散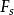 梯度擴散
梯度擴散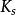 梯度擴散
梯度擴散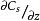 梯度擴散
梯度擴散式中 是某物理屬性s的通量密度, 是共擴散係數, 是其濃度梯度。
在近地大氣層中,動量、熱量和水蒸氣通量的梯度擴散計算方法可用下列公式表示:
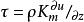 梯度擴散
梯度擴散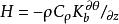 梯度擴散
梯度擴散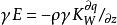 梯度擴散
梯度擴散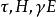 梯度擴散
梯度擴散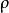 梯度擴散
梯度擴散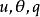 梯度擴散
梯度擴散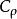 梯度擴散
梯度擴散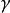 梯度擴散
梯度擴散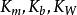 梯度擴散
梯度擴散式中 相應為空氣應力(動量輸送)、熱量和水汽通量, 為平均空氣密度(應為乾空氣和水汽密度之和), 為平均風速、位溫和比濕, 為空氣定壓比熱, 為水汽潛熱係數,z為高度, 為動量、熱量和水汽的湍流擴散係數,它們取決於風的切熱和熱力層結,即:
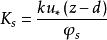 梯度擴散
梯度擴散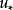 梯度擴散
梯度擴散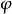 梯度擴散
梯度擴散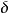 梯度擴散
梯度擴散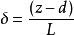 梯度擴散
梯度擴散其中s代表m、h或W,k是Von Karman常數,取值為0.4; 為摩擦速度;d為零面位移高度; 為無因次穩定度 的函式, ,L為Monin-Obukhov長,定義為:
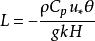 梯度擴散
梯度擴散其中g為重力加速度。
研究進展
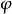 梯度擴散
梯度擴散微氣象研究的一個重要方面,就是在尋求 的經驗函式形式。目前大多數近地層物理硏究所採用的是所謂Dyer- Businger公式:
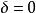 梯度擴散
梯度擴散(1)中性條件下( ):
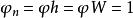 梯度擴散
梯度擴散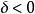 梯度擴散
梯度擴散(2)不穩定條件下( ):
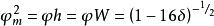 梯度擴散
梯度擴散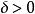 梯度擴散
梯度擴散(3)穩定條件下( ):
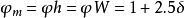 梯度擴散
梯度擴散