定義
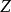 條件獨立性
條件獨立性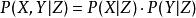 條件獨立性
條件獨立性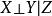 條件獨立性
條件獨立性給定第三個事件 ,如果 ,則稱X和Y是條件獨立事件,符號表示為。
若X,Y關於事件Z條件獨立,則有以下一些理解:
(1)事件 Z 的發生,使本來可能不獨立的事件A和事件B變得獨立起來;
(2)事件Z 的出現或發生,解開了X 和 Y 的依賴關係。
結論
若 X,Y關於事件Z條件獨立,則P(X|Y,Z)=P(X|Z)
證明:
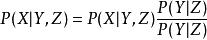 條件獨立性
條件獨立性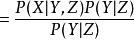 條件獨立性
條件獨立性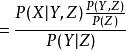 條件獨立性
條件獨立性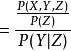 條件獨立性
條件獨立性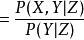 條件獨立性
條件獨立性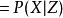 條件獨立性
條件獨立性示例
給定三個事件X,Y,Z:
•X:明天下雨;
•Y:今天的地面是濕的;
•Z:今天是否下雨;
Z事件的成立,對X和Y均有影響,然而,在Z事件成立的前提下,今天的地面情況對明天是否下雨沒有影響。即,在已知Z的前提下,X和Y是相互獨立的,即X和Y是條件獨立的。
套用
圖模型可視化地表示變數間地相互影響,並且它有一個優點:利用條件獨立性可以將大量變數上的推斷分解成一組涉及少量變數的局部計算。
在圖模型中,條件獨立有以下三種典型情況:
(1)頭到尾連線
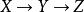 條件獨立性
條件獨立性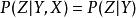 條件獨立性
條件獨立性三個事件可以順序連線,如。若給定Y,則X與Z是獨立的:知道Y就知道Z的一切;知道X的狀態並不能為Z增加附加知識,記作。一般說,Y阻塞(block) 了從X到Z的路徑,換句話說,Y分開了X和Z,意指如果刪掉Y,則就不存在X和Z之間的路徑。在這種情況下,聯合機率寫作:
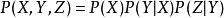 條件獨立性
條件獨立性典型地,X是Y的原因,Y是Z的原因。
(2)尾到尾連線
X可能是兩個節點Y和Z的父節點,聯合密度可以寫作:
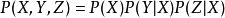 條件獨立性
條件獨立性通常,Y和Z是通過X依賴的,給定X,則它們變成獨立的
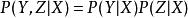 條件獨立性
條件獨立性當X的值已知時,它阻塞了Y和Z之間的路徑,換言之,X分開了Y和Z。
(3)頭到頭連線
在頭到頭連線中,有兩個父節點X和Y連線到單個節點Z,則聯合密度記作:
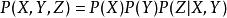 條件獨立性
條件獨立性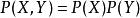 條件獨立性
條件獨立性X和Y是獨立的:。當知道Z時,X和Y變成依賴的。這種情況與阻塞或分開的概念不同。當觀察不到Z時,X和Y之間的路徑被阻塞;當Z(或者它的任意後代)被觀測到時,X和Y便不再是阻塞的、獨立的。
