核能級壽命測量
正文
原子核被激發後,可以在較高的能級上停留一段時間,此時間稱為該能級的壽命。實驗上測到的壽命是激發核(處在激發態的核)能級的平均壽命, 用τ表示。激發核是不穩定核,往往通過γ輻射向低能級或基態躍遷。躍遷幾率λ=1/τ(見γ躍遷)。實驗上測定τ之後,即可同採用某種核模型波函式計算的λ 比較,從而達到檢驗理論的目的。測量τ 的方法有間接和直接測量兩類。間接測量方法如庫侖激發、γ共振、電子非彈性散射、同K系X射線壽命的比較等。直接測量法有延遲符合法、都卜勒效應法、阻塞效應法等。
延遲符合法 級聯γ射線的中間態有一定的壽命,可以用測量這兩條γ射線之間的延遲符合時間譜,去確定中間態的壽命;或者是利用加速器的脈衝束流,測量在脈衝束間隔內的延遲時間譜,以求出能級的平均壽命。這兩種方法測量的時間範圍一般在10-3~10-10s(符合技術見符合和反符合系統)。
都卜勒效應法 如果核反應A(a,b)B*在薄靶中進行,則生成的激發核B*按動量守恆定律將以速度v(0)在真空中反衝。B*在反衝飛行中放出的γ射線能量E γ和在停止時放出的γ射線能量
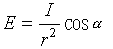 之間有都卜勒移動,而
之間有都卜勒移動,而  , (1)
, (1)
 求出τ。這種方法稱為反衝距離法(RDM)。此法要求所測的τ值大於B*在阻止物質中的特徵慢化時間α【即具有速度 v(0)的B*的數目降到為原來的1/e的時間,一般α≈5×10-13s。
求出τ。這種方法稱為反衝距離法(RDM)。此法要求所測的τ值大於B*在阻止物質中的特徵慢化時間α【即具有速度 v(0)的B*的數目降到為原來的1/e的時間,一般α≈5×10-13s。 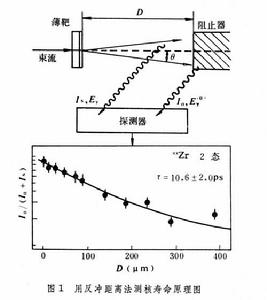 核能級壽命測量
核能級壽命測量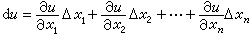 。 (2)
。 (2)
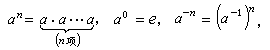 時,式(2)可以寫成
時,式(2)可以寫成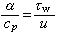 。 唕γ是γ 射線的平均能量,v(0)是初始速度。若θ1在和θ2角度處分別測量,則可利用
。 唕γ是γ 射線的平均能量,v(0)是初始速度。若θ1在和θ2角度處分別測量,則可利用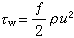 得到F(τ)的測量值,式中ΔE是在兩個角度處測量的γ射線能量移動。另外,在近似情況下由 F(τ)=α/(α+τ)可得到F(τ)的計算值,將二者加以比較,從而得到最佳的τ。②因反衝速度v(t)是時間t的函式,其數值從 v(0)衰減到零,所以測量的γ射線能量也在
得到F(τ)的測量值,式中ΔE是在兩個角度處測量的γ射線能量移動。另外,在近似情況下由 F(τ)=α/(α+τ)可得到F(τ)的計算值,將二者加以比較,從而得到最佳的τ。②因反衝速度v(t)是時間t的函式,其數值從 v(0)衰減到零,所以測量的γ射線能量也在 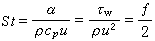 和
和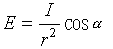 之間有一個分布。如果能級壽命很短,則在反衝核未停止之前多已衰變, 放出的γ射線能量多接近完全移動時放出的能量
之間有一個分布。如果能級壽命很短,則在反衝核未停止之前多已衰變, 放出的γ射線能量多接近完全移動時放出的能量 。如果能級壽命很長,則多數反衝核只有在被阻止後才衰變,放出γ射線的能量多接近
。如果能級壽命很長,則多數反衝核只有在被阻止後才衰變,放出γ射線的能量多接近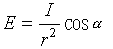 。如圖2可見,能量分布圖形同核能級壽命τ有關。因此從Eγ 的分布圖形可以決定τ。
。如圖2可見,能量分布圖形同核能級壽命τ有關。因此從Eγ 的分布圖形可以決定τ。  核能級壽命測量
核能級壽命測量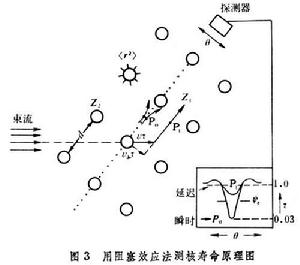 核能級壽命測量
核能級壽命測量參考書目
A. Z. Schwarzschild and E.K.Warburton, Ann.Rev. Nucl.Sci., Vol. 18, p.265, 1968.
W.W.Gibson,Ann.Rev.Nucl.Sci.,Vol.25,P.465, 1975.

