柯爾莫哥洛夫定理

柯爾莫哥洛夫定理是關於Lp[a,b]的子集為列緊集的特徵的定理。

定義

柯爾莫哥洛夫定理是關於L [a,b]的子集為列緊集的特徵的定理。

充要條件

L [a,b](p≥1)中集A為列緊集的充分必要條件如下：

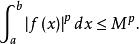柯爾莫哥洛夫定理

1、存在常數M，使對任意f(x)∈A，有

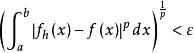柯爾莫哥洛夫定理

2.對任意ε>0，存在δ>0，只要0<h<δ，對任意f(x)∈A，都有，這裡

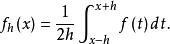柯爾莫哥洛夫定理

列緊集

列緊集是度量空間中的一類子集，設A是度量空間X中的無窮集，如果A中的任一無窮子集必有一個收斂的點列，就稱A是X中的列緊集；如果X本身是列緊集，就稱X是列緊距離空間，簡稱為列緊空間。

列緊集是有界的。需要注意的是，一般度量空間與歐氏空間不同，有界閉集一定列緊。