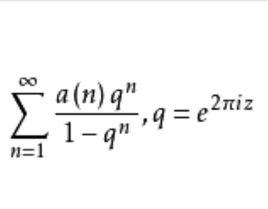基本介紹
定義1 定義級數
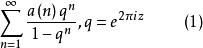 朗伯級數
朗伯級數為 朗伯(Lambert)級數 。
一方面,將(1)展成Fourier級數
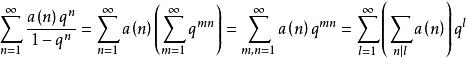 朗伯級數
朗伯級數艾森斯坦(Eisenstein)級數E(z)的Fourier展開式為
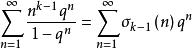 朗伯級數
朗伯級數故
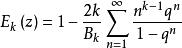 朗伯級數
朗伯級數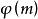 朗伯級數
朗伯級數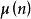 朗伯級數
朗伯級數對於歐拉函式以及麥比烏斯函式,對應有
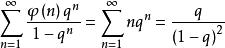 朗伯級數
朗伯級數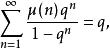 朗伯級數
朗伯級數它們分別表示
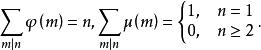 朗伯級數
朗伯級數另一方面,若給出了Fourier級數,則可將其改為朗伯級數
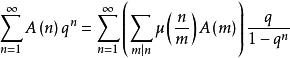 朗伯級數
朗伯級數這個變換是麥比烏斯逆變換
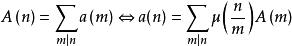 朗伯級數
朗伯級數相關介紹
研究朗伯級數是為了給自守形式的表示提供方便,拉馬努金計算了許多朗伯級數的值,其中較為著名的有如下幾個,稱為拉馬努金等式 。
拉馬努金等式
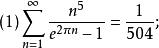 朗伯級數
朗伯級數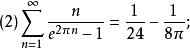 朗伯級數
朗伯級數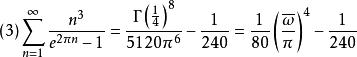 朗伯級數
朗伯級數下面給出等式(1)的證明。
由E(z)的變換公式有
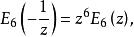 朗伯級數
朗伯級數將z=i代入得
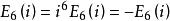 朗伯級數
朗伯級數所以E(i)=0,另一方面,根據Fourier展開式有
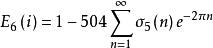 朗伯級數
朗伯級數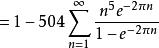 朗伯級數
朗伯級數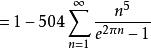 朗伯級數
朗伯級數從而(1)式得證 。