有序樣品聚類法的概念
系統聚類法，被分類的樣品是相互獨立的，分類時彼此是平等的。而有序樣品分類法要求樣品按一定的順序排列，分類時是不能打亂次序的，即同一類樣品必須是互相鄰接的。比如要將新中國成立以來國民收入的情況劃分為幾個階段，此階段的劃分必須依年份的順序為依據，又如研究天氣演變的歷史時，樣品是按從古到今的年代排列的，年代的次序也是不能打亂的。
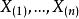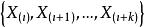有序樣品聚類法
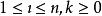有序樣品聚類法
有序樣品聚類法
有序樣品聚類法如果用 表示n個有序的樣品，則每一類必須是這樣的形式： ，其中， 且 ，即同一類樣品必須是相互鄰接的。研究這樣分類問題稱為 有序樣品的聚類法，該方法是由Fisher在1958年提出的。
有序樣品的分類實質上是找一些分點，將有序樣品劃分為幾個分段，每個分段看作一個類，所以分類也稱為分割。顯然分點取在不同的位置就可以得到不同的分割。通常尋找最好分割的一個依據就是使各段內部樣品之間的差異最小，而各段樣品之間的差異較大，所以有序樣品聚類法又稱為 最優分割法。
最優分割法的計算步驟
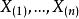有序樣品聚類法
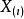有序樣品聚類法設有序樣品依次為 ，( 為p維向量)
(1)定義類的直徑
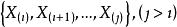有序樣品聚類法設某一類G包含的樣品有 ，記
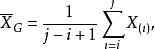有序樣品聚類法
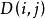有序樣品聚類法用 表示這一類的直徑，常用的直徑有：
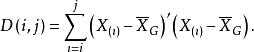有序樣品聚類法當p=1時，有時用直徑為：
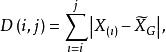有序樣品聚類法
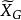有序樣品聚類法其中， 是這一類數據的中位數。
(2)定義分類的損失函式(或稱目標函式、誤差函式等)
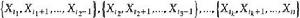有序樣品聚類法用b(n，k)表示將n個有序樣品分為k類的某一種分法，常記分法b(n，k)為： 或簡記為：
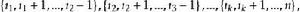有序樣品聚類法
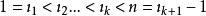有序樣品聚類法
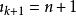有序樣品聚類法其中分點為： 即 。
定義這種分類法的損失函式為：
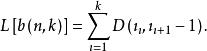有序樣品聚類法
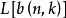有序樣品聚類法 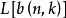有序樣品聚類法當n，k固定時， 越小表示各類的離差平方和越小，分類是合理的。因此要尋找一種分法b(n，k)，使分類損失函式L達最小，記P(n，k)是使 達極小的分類法。
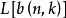有序樣品聚類法(3) 的遞推公式
Fisher算法最核心的部分是利用以下兩個遞推公式：
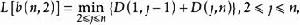有序樣品聚類法
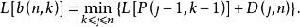有序樣品聚類法
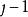有序樣品聚類法
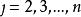有序樣品聚類法以上兩公式由定義即可證明。其中第二式表示，若要找將n個樣品分為k類的最優分割，應建立在將 個樣品分為k-1類的最優分割基礎上(這裡 )。
(4)最優解求法
若分類數k(1<k<n)，求分類法p(n，k)使它在損失函式意義下達最小，其求法如下：
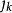有序樣品聚類法
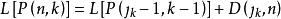有序樣品聚類法
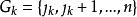有序樣品聚類法
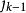有序樣品聚類法
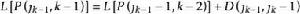有序樣品聚類法
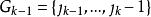有序樣品聚類法
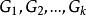有序樣品聚類法
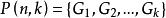有序樣品聚類法首先，找分點 使 達最小，於是得第k類 ，然後，找 ，使它滿足 ，得到第k-1類 ，類似的方法依次可得到所有類 ，這就是所求的最優解，即 。
總之，最優分割法分類的依據是離差平方和，而算法的核心部分是兩個遞推公式 。
