定義
最短路徑樹
最短路徑樹
最短路徑樹 最短路徑樹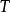 最短路徑樹 最短路徑樹
最短路徑樹 最短路徑樹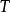 最短路徑樹 最短路徑樹考慮一個連通無向圖 ，一個以頂點 為根節點的最短路徑樹 是圖 滿足下列條件的生成樹——樹 中從根節點 到其它頂點 的路徑距離，在圖 中是從 到 的最短路徑距離。
在一個所有最短路徑都明確（例如沒有負長度的環）的連通圖中，我們可以使用如下算法構造最短路徑樹：
最短路徑樹使用Dijkstra算法或Floyd算法計算圖 G 中從根節點 v 到 頂點 u 的最短距離 。
最短路徑樹 最短路徑樹
最短路徑樹 最短路徑樹
最短路徑樹
最短路徑樹 最短路徑樹 最短路徑樹 最短路徑樹對於所有的非根頂點 ，我們可以給 分配一個父頂點 ， 連線至u且 。當有多個 滿足條件時，選擇從v到 的最短路徑中邊最少的 。當存在零長度環的時候，這條規則可以避免循環。
用各個頂點和它們的父節點之間的邊構造最短最短路徑樹。
最短路徑樹上面的算法保證了最短路徑樹的存在。像最小生成樹一樣，最短路徑樹通常也不只有一個的。在所有邊的權重都相同的時候，最短路徑樹和廣度優先搜尋樹一致。在存在負長度的環時，從 到其它頂點的最短簡單路徑不一定構成最短路徑樹。
相關算法
Dijkstra算法
設定兩個定點的集合T和S，集合S中存放已找到最短路徑的定點，集合T中存放當前還未找到的最短路徑的定點。初始狀態時，集合S中只包含源點v0然後不斷從集合T中選取到定點v0路徑長度最短的頂點u加入集合S，集合S中每加入一個新的頂點u，都要修改定點v0到集合T中剩餘頂點的最短路徑長度值，集合T中每個頂點新的最短路徑長度值為原來的最短路徑長度值與定點u的最短路徑長度值加上u到該頂點的路徑長度值中的較小值。此過程不斷重複，直到集合T的頂點全部加入到集合S為止 。
Floyd算法
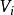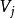最短路徑樹
最短路徑樹從代表任意兩個節點 到 距離的帶權鄰接矩陣D(0)開始，首先計算D(1)，即計算Vi到Vj經過一次經轉的所有可能路徑，經過比較後選出最短路，代替D(0)中對應的路徑，疊代列出距離矩陣D(1)，D(1)中各元素表示通過一次疊代後網路中任意兩點間最短路，也即網路中任意兩點之間直接到達或只經過一個中間點時的最短路。在此基礎上依次計算D(2)，D(3)，…，D(k)，D(k)中對應的元素表示任意兩點間不經過中間點或最多允許經過2k+1箇中間點時的最短路。當D(k+1)=D(k)時，表明得到的帶權鄰接矩陣D(k)就反映了所有頂點對之間的最短距離信息，成為最短距離矩陣。
