定律定義
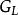 最優匹配
最優匹配推導過程設L是完備的二部賦權圖G=(X,Y,E,F)的可行點標記,若M*是 的完美匹配,則M*是G的權數最大的匹配。稱為最優(或最佳)匹配。
相關概念
1、令M是圖G的邊子集,若M中任意兩條邊都沒有共同的結點,則稱M是G的一個匹配;其中與M的邊關聯的結點稱為飽和點,否則成為非飽和點。 2 、設M是G=(V,E)的一個匹配,若對G的任意匹配M'都有|M|>=|M'|,則稱M是G的一個最大匹配。 3、給定了G的一個匹配M,G中屬於M與不屬於M的邊交替出現的道路稱為互動道路。 4、設P是G中關於匹配M的一條互動道路,若P的兩個端點是關於M的非飽和點,則它就稱為可增廣道路。 5、M是G的最大匹配若且唯若G中不存在關於M的可增廣道路。 6、設r是二分圖G的最大匹配數,s是其鄰接矩陣的最小覆蓋數,則有r==s。 實際意義 指派問題:需要完成n1項任務,有n2個人可以承擔這些任務。由於每個人的專長不同,完成不同任務的成本與效率也不同。應如何分配任務才能使得總成本最小或者總效益最大。 算法及步驟 使用匈牙利算法求解最佳匹配問題,基於最小成本的問題求解。 時間複雜度O(m×n)。 step1:使效益矩陣經過變換,在各行各列中都出現0元素 (1)效益矩陣每行的元素減去該行的最小元素; (2)再將所得的效益矩陣每列的元素減去該列的最小元素。 step2:進行指派,尋求最優解 (1)從只有一個0元素的行(列)開始,給這個0元素加圈,這表示對這行所代表 的人而言,只有一種任務可以指派。然後划去該加圈0元素所在列(行)的其他0元素,表示該列所代表的任務已經指派完,無需考慮其他人。 (2)給只有一個0元素的列(行)的0元素加圈,同時划去該0元素所在行(列)的其他0元素。 (3)重複進行(1)、(2)兩步,直至所有0元素都被加圈或划去為止。 (4)若仍存在未加圈未划去的0元素,且同行(列)的0元素至少有兩個(表示對這個可以從兩項任務中指派其一),則對同行同列中其他0元素總數最少的0元素加圈(表示選擇性多的要禮讓選擇性少的),並划去同行同列中的其他0元素。可反覆進行,直至所有0元素都被加圈或划去為止。 (5)若加圈的0元素數量m等於矩陣的階數n(這裡矩陣的階數指成本/效益矩陣行數、列數中的較小值),則指派問題已經得到最優解;若m<n,則轉step3。 step3:作最少的直線覆蓋所有 的 0元素,以確定成本/效益矩陣中的獨立0元素 (1)對沒有加圈0元素的行打勾; (2)對已打勾的行中被划去0元素所在列打勾; (3)對打勾的列中的加圈0元素所在行打勾; (4)重複(2)、(3)直至找不出新的可打勾的行、列為止; (5)選取未打勾的行和已打勾的列,即可覆蓋全部0元素。 (6)選取的行、列數之和(即所作直線數)為l。若l<n,說明必須再變換當前的成本/效益矩陣才能找到n個獨立的0元素,為此轉step4;若l==n而m<n,則返回 step2的(4),另行試探。 step4: 增加 獨立的0 元素 在未被直線覆蓋的部分中找出最小元素。在打勾的行的各元素減去該最小元素,在打勾的列的各元素加上該最小元素,以保證原來的0元素不變。刪除所有打勾、加圈、划去記號,返回step2。