明安圖（？～約1764）
正文
中國清代數學家、天文學家。字靜庵。蒙古族正白旗人。生年不詳，約卒於乾隆二十九年。少年時為官學生,後被選派至欽天監,專門學習天文、曆法和數學。當時康熙帝正熱衷於學習和研究科學技術，因此，他也常有機會入宮聽講。康熙五十一年(1712)，康熙帝至避暑山莊,有一批著名科學家隨行,他是隨行人員中惟一列名的官學生。康熙帝曾親自就天文數學問題進行提問，並解答他所提出的問題。結業後，畢生在欽天監作，曾任欽天監時憲科五官正近四十年，主要負責推算日月五星運行，編訂時憲書（即民用曆書），以及主持時憲書滿蒙文本的翻譯等。乾隆二十四年(1759)，升任欽天監監正。在天文學方面，他參加了三部重要天文學著作的編著。第一部為《曆象考成》，他擔任考測工作。該書分上下兩編,共42卷,主要成就是在實測方面，如根據實測改進了第谷體系的黃赤交角數據等。第二部為《曆象考成後編》，共10卷。其理論、算法和所用數據都比《曆象考成》有很大進步。他任該書副總裁和彙編，是該書的主要作者之一。第三部為《儀象考成》，共32卷他擔任推算工作。該書介紹了新製造的大型天文儀器璣衡撫辰儀的性能和用法。它所載錄的星表，是在實測和推算的基礎上編成的，記錄了3083顆恆星的黃道坐標和赤道坐標，達到了當時的世界先進水平。 明安圖在數學上有很深的造詣，特別是對三角函式和反三角函式的冪級數展開式問題,進行了深入研究,獲得了豐碩成果。清初，法國傳教士杜德美曾向中國學者介紹了三個無窮級數公式，但沒有給出證明。這三個公式為π的無窮級數公式，正弦和正矢的冪級數展開式： ① 圓徑求周
；
。
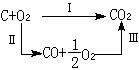
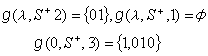
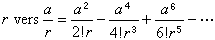
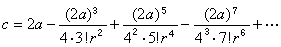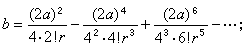
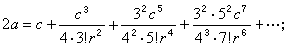
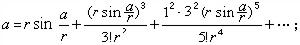
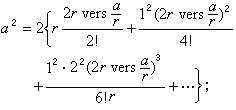
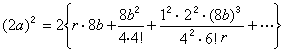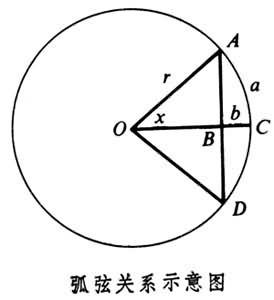）。他曾自述：“以上九法，皆至精至密,任有圓線求直線,有直線求圓線，雖推至無窮，靡不合也。” 明安圖的數學成就總結在《割圓密率捷法》一書中。該書共四卷，卷一“步法”，羅列了所得到的各無窮級數公式，卷二“用法”，系各公式在數學和天文學問題上的套用，卷三、四為“法解”上、下，闡述了各公式的證明方法。這部著作在他生前只完成一部分，後由其學生陳際新、張肱、其子明新續成(1774)。他的成就和所創立的方法，對於清代冪級數研究領域產生了很大影響。明安圖在測繪地圖方面也有重要貢獻，乾隆二十一年(1756)和二十四年(1759)，他兩次親往新疆測繪地圖，完成了準噶爾地區和天山南部地區的測量與繪圖任務。著名的《乾隆內府輿圖》就是在《康熙皇輿全圖》和這兩次實地測量的基礎上繪製而成的。
