定義
在經典力學與幾何學裡,所有環繞著三維歐幾里得空間的原點的旋轉,組成的群,定義為 旋轉群。根據定義,環繞著原點的旋轉是一個保持矢量長度,保持空間取向(遵守右手定則或 左手定則)的線性變換。假若,一個線形變換保持矢量長度,逆反空間取向,則稱此變換為假旋轉。
兩個旋轉的複合等於一個旋轉。每一個旋轉都有一個獨特的逆旋轉;零角度的旋轉是單位元。旋轉運算滿足結合律.由於符合上述四個要求,所有旋轉的集合是一個群。更加地,旋轉群擁有一個天然的流形結構。對於這流形結構,旋轉群的運算是光滑的;所以,它是一個李群。旋轉群時常會用 SO(3) 來表示。
長度與角度
除了保持長度(保長),旋轉也保持矢量間的角度(保角)。原因是兩矢量 u和 v的內積可寫作:
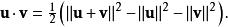 旋轉群
旋轉群R中的保長轉換保持了標量內積值不變,也因此保持了矢量間的角度。包括SO(3)在內的一般性情形,參見典型群。
旋轉軸
三維空間中非平凡的旋轉,皆繞著一個固定的“旋轉軸”,此旋轉軸是 R的特定一維線性子空間(參見:歐拉旋轉定理)。旋轉作用在與旋轉軸正交的二維平面,如同尋常的二維旋轉。既然二維旋轉皆可以旋轉角φ表示,則任意三維旋轉則可用旋轉軸搭配旋轉角來表示。
舉例來說,繞著正 z軸旋轉φ角的逆時針旋轉為
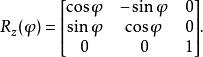 旋轉群
旋轉群給定 R中一單位矢量 n以及角度φ,設 R(φ, n)代表繞 n軸作角度φ的逆時針旋轉,則:
•R(0,n)為相等轉換(identity transformation),n任意單位矢量;
•R(φ,n) =R(−φ, −n);
•R(π + φ,n) =R(π − φ, −n)。
利用這些特性,參數為旋轉角φ(範圍: 0 ≤ φ ≤ π)與單位矢量 n的任意旋轉有如下性質:
•若φ = 0,n可為任意單位矢量;
•若0 < φ < π,n為特定單位矢量;
•若φ = π,n為彼此反向的兩特定單位矢量;亦即,旋轉R(π, ±n)是等價的。
有限子群
SO(3)中只有很少的幾個有限子群,且它們全部是熟悉的對稱群,包括有:
•C:繞一條直線轉過角度2π/k的倍數的旋轉的循環群
•D:正k邊形的二面體群
•T:將正四面體映為自身的十二個旋轉四面體群
•O:立方體或正八面體旋轉的24階八面體群
•I:正十二面體或正二十面體的60個旋轉的二十面體群
套用
常見的三維旋轉群有如下幾種:
正六面體:階24, 頂點8個,面6個,棱12條,均為正方形
| 轉動群 | 頂點 | 面 | 棱 | 個數 |
| 不動 | (1)^8 | (1)^6 | (1)^12 | 1 |
| 面心-面心, ±90度 | (4)^2 | (1)^2 (4) | (4)^3 | 6 |
| 面心-面心180度 | (2)^4 | (1)^2 (2)^2 | (2)^6 | 3 |
| 棱心-棱心180度 | (2)^4 | (2)^3 | (1)^2 (2)^5 | 6 |
| 空間對角線±120度 | (3)^2 (1)^2 | (3)^2 | (3)^4 | 8 |
正八面體:階24, 頂點6個,面8個,棱12條,均為等邊三角形
| 轉動群 | 頂點 | 面 | 棱 | 個數 |
| 不動 | (1)^6 | (1)^8 | (1)^12 | 1 |
| 頂點-頂點 ±90度 | (1)^2 (4) | (4)^2 | (4)^3 | 6 |
| 頂點-頂點 180度 | (1)^2 (2)^2 | (2)^4 | (2)^6 | 3 |
| 棱心-棱心 180度 | (2)^3 | (2)^4 | (1)^2 (2)^5 | 6 |
| 面心-面心 ±120度 | (3)^2 | (3)^2 (1) | (3)^4 | 8 |
正十二面體:階60, 頂點20個,面12個,棱30條,均為正五邊形
| 轉動群 | 頂點 | 面 | 棱 | 個數 |
| 不動 | (1)^20 | (1)^12 | (1)^30 | 1 |
| 面心-面心±72,±144度 | (5)^4 | (1)^2 (5)^2 | (5)^6 | 24 |
| 棱心-棱心180度 | (2)^10 | (2)^6 | (1)^2 (2)^14 | 15 |
| 頂點-頂點±120度 | (1)^2 (3)^6 | (3)^4 | (3)^10 | 20 |
正二十面體:階60, 頂點12個,面20個,棱30條,均為等邊三角形
| 轉動群 | 頂點 | 面 | 棱 | 個數 |
| 不動 | (1)^12 | (1)^20 | (1)^30 | 1 |
| 頂點-頂點±72,±144度 | (1)^2 (5)^2 | (5)^4 | (5)^6 | 24 |
| 棱心-棱心180度 | (2)^6 | (2)^10 | (1)^2 (2)^14 | 15 |
| 面心-面心±120度 | (3)^4 | (1)^2 (3)^6 | (3)^10 | 20 |
足球:階60, 頂點60個,面32個,棱數90條,20個正六邊形,12個正五邊形
| 轉動群 | 頂點 | 面 | 棱 | 個數 |
| 不動 | (1)^60 | (1)^32 | (1)^90 | 1 |
| 五邊形面心-五邊形面心±72,±144度 | (5)^12 | (1)^2 (5)^6 | (5)^18 | 24 |
| 六邊形面心-六邊形面心±120度 | (3)^20 | (1)^2 (3)^10 | (3)^30 | 20 |
| 正六邊形棱中-棱180度(這種棱有30條) | (2)^30 | (2)^16 | (1)^2 (2)^44 | 15 |
類足球(正八面體切掉角):階24,頂點24個,面14個,棱數36條,8個正六邊形,6個正方形
| 轉動群 | 頂點 | 面 | 棱 | 個數 |
| 不動 | (1)^24 | (1)^14 | (1)^36 | 1 |
| 正方形面心-正方形面心±90度 | (4)^6 | (1)^2 (4)^3 | (4)^9 | 6 |
| 正方形面心-正方形面心180度 | (2)^12 | (1)^2 (2)^6 | (2)^18 | 3 |
| 六邊形面心-六邊形面心±120度 | (3)^8 | (1)^2 (3)^4 | (3)^12 | 8 |
| 六邊形棱中-六邊形棱中180度 | (2)^12 | (2)^7 | (1)^2 (2)^17 | 6 |

