斯塔克爾貝格對策
正文
對策論中的多級遞階決策問題，又稱主從對策，由經濟學家 H.von斯塔克爾貝格提出。社會現象的結局通常是由許多決策人的行動共同決定的。而這些決策人分居不同層次，形成所謂多級遞階的決策系統。上層決策人具有一定權威，起著主導作用，有時代表全局的利益。他們對整個系統的控制可以通過操縱一些“槓桿”變數來影響下級的行為而實現。例如，用國家調節利率、稅收、投資等決策量來控制各部門各單位的行為而實現全局最優，企業通過分配、獎勵等手段來引導職工採取合作行為以提高整體的效益,都屬於主從對策。以下標L表示主導者,xL、zL、xL＝γL(zL)和KL分別表示主導者的決策變數、信息、策略和目標函式。以下標 F表示隨從者，隨從者的對應量為xF、zF、xF＝γL(zF)和KF。斯塔克爾貝格決策問題就是上級如何選擇並宣布他的策略γL,使下級對此γL的理性回響最符合上級的需要。在最簡單的情況下,上級只能決定並預先宣布一個xL的值,力圖獲得最好的結果。這時F根據他的信息zF＝xL選擇xF,使KF最大，即xF＝γF(xL)＝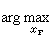
KF(xL，xF)
KL＝KL(xL，xF)＝KL(xL，γF(xL))
因此 L可通過選擇xL使KL最大。對主從對策理論的深入研究主要是在70年代以後進行的。主從對策可分為靜態和動態兩類。靜態主從對策 靜態情形下雙方都只作一次決策。如L只選一個參數xL，宣布之後F進行決策並確定xF,然後雙方一起執行。只要L確實說到做到,這種預期的結果就必然出現。因此這種解是穩定的。如果 L採用欺騙手法，例如宣布
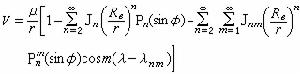，由於預計到F的回響將為
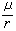，而實際上卻採取 
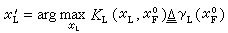決策以牟取更多利益。結果，由於雙方都是“理性人”，都能進行合理的推理和計算，F也能預見到L的做法，他就會在一次性行動時亮出
。同樣L又預見到這點而採用
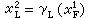，然後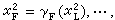
等等。這種循環猜測過程無限繼續下去，如果收斂到極限值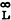(x
,x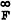
),則滿足:
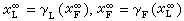)。這實際上就是非合作的納什平衡解。對L來說這個結局往往不如主從對策好，這說明L的欺騙行為對己也不利,從而也說明主從對策的基本假定是合理的、成立的。在靜態主從對策中套用最廣泛的是二次對策，即KL和KF是決策量的二次函式，而且各約束條件均為線性關係，這時較易於求解。 動態主從對策 動態主從對策的一般模型包含一個狀態演化過程：
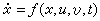
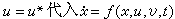)和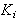
之後解出使KF為最大的v*(即最優控制問題)，問題歸結為如何選擇u*使所解出的 v*恰好使KL也達到最大(相對於 u的其他選擇而言)。這樣得到的u* 和v* 就是動態主從對策的解。動態主從對策的雙方可採用的決策形式依他們擁有的信息不同而不同，大致可分為開環策略、無記憶狀態反饋策略和有記憶狀態反饋的閉環策略。這些決策形式表示決策人利用信息反饋，靈活反應以改進自身地位的可能性。動態主從對策在理論上是個難題，在計算上也十分複雜。但它揭示了各種信息結構對結局的影響（即開環、反饋、閉環解之間的差別），有一定理論意義，同時也有很大的實際套用價值。