簡介
經典斯特姆-利烏維爾變換理論是由傑克斯·查爾斯弗朗索瓦斯特姆（1803年至1855年）和約瑟夫·利烏維爾（1809年至1882年）提出的。
19世紀，隨著各種曲線坐標系的引入和新的函式類如貝塞爾(Bessel)函式、勒讓德(Legendre)多項式等作為常微分方程的特徵函式而興起，確定帶邊界條件的常微分方程的特徵值與特徵函式，便成為日益突出的重要問題。利烏維爾和他的朋友、力學教授斯圖姆(Sturm)在30年代同時鑽研了這類問題。
定義
二階微分方程在物理學和科學技術中有廣泛的套用，同時也是研究高階微分方程與數學物理方程的基礎。在最一般的情況下解變係數二階微分方程又是很困難的，至今沒有普遍的方法。
此外，在實際套用中，並非求得通解就可以解決問題，還必須根據具體情況解初值問題、邊值問題及特徵值問題。即使對二階常係數含參數的齊次常微分方程，甚至同一方程在不同的邊界條件下，解的情況也是千差萬別。
因此，我們不僅討論一般的特徵值問題，而且討論那些最常遇到的，在數學物理中有廣泛套用的特徵值問題，這就是Sturm—Liouville問題。
過程
利烏維爾和斯圖姆考慮了由變密度棒的熱傳導過程引出的二階常微分方程，採用逐次逼近法表達其解：
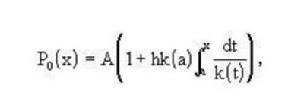斯圖姆與利烏維爾變換
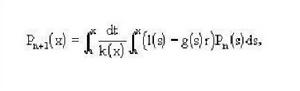斯圖姆與利烏維爾變換這樣，就得到了關於微分方程解的存在性的第一條定理，它發表在1838年3卷1期的《套用數學雜誌》，逐次逼近法成為求解常微分方程的一種典型方法，上述邊值問題則被稱為斯圖姆-利烏維爾問題。
隨後，兩人著眼於更一般的二階微分方程，
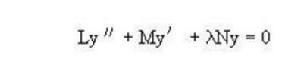斯圖姆與利烏維爾變換
斯圖姆與利烏維爾變換其中L，M，N是x的連續函式， 是參數，它可以改寫成
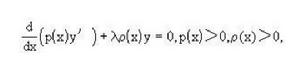斯圖姆與利烏維爾變換他們證明了下列基本結果：
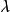斯圖姆與利烏維爾變換
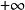斯圖姆與利烏維爾變換
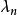斯圖姆與利烏維爾變換1、僅當 取遞增到 的正數序列{ }的任一值時，原問題才有解；
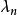斯圖姆與利烏維爾變換
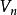斯圖姆與利烏維爾變換 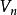斯圖姆與利烏維爾變換
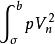斯圖姆與利烏維爾變換2、對於每一個 ，解是一函式 的倍數，而 可用條件 ；
令dx=1加以規範化；
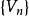斯圖姆與利烏維爾變換
斯圖姆與利烏維爾變換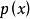
斯圖姆與利烏維爾變換
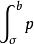斯圖姆與利烏維爾變換3、 在 上組成具有權函式 的一個正交函式系
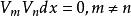斯圖姆與利烏維爾變換後來，在法蘭西學院的教學中，利烏維爾又引入了伴隨邊值條件(adjoint boundary values)的概念，將斯圖姆-利烏維爾理論，尤其是斯圖姆關於特徵函式的有關結論推廣到非自伴隨高階方程上。利烏維爾在擴展導數定義時，除了將被導函式先展開為指數級，還利用過拉亞拉斯積分展開式的方法：
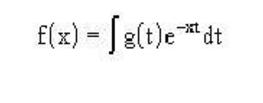斯圖姆與利烏維爾變換在證明了
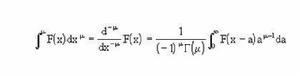斯圖姆與利烏維爾變換等幾個重要公式後，利烏維爾展開了如何用其解決幾何、力學問題中產生的積分方程：把積分方程變成求導問題，最後得到的微分方程是可解的。
在斯圖姆-利烏維爾理論中涉及的則是另一種不同類型的方程，即希爾伯特第二類積分方程。它有如下形式：
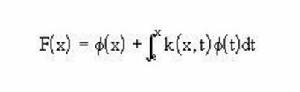斯圖姆與利烏維爾變換通過解積分方程得到微分方程的解，這是斯圖姆-利烏維爾理論最有意義的一點。而微分方程與積分方程之間的內在聯繫通過他們的上述努力也愈加清晰了。
特徵值問題
描述
一般的二階斯圖姆-利烏維爾問題是以下形式的特徵值問題：
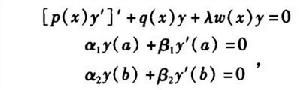斯圖姆與利烏維爾變換
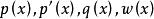斯圖姆與利烏維爾變換
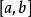斯圖姆與利烏維爾變換 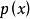斯圖姆與利烏維爾變換
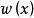斯圖姆與利烏維爾變換 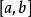斯圖姆與利烏維爾變換
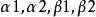斯圖姆與利烏維爾變換
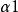斯圖姆與利烏維爾變換
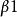斯圖姆與利烏維爾變換
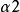斯圖姆與利烏維爾變換
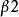斯圖姆與利烏維爾變換其中 在 上可積，且 和 在 上大於0。這裡 都是實常數。此外， 和 不同時為0， 與 不同時為0。
斯圖姆-利烏維爾問題具有其理想的特點，這種特點是一般的特徵值問題所沒有的。
定理
1、斯圖姆-利烏維爾問題的特徵值問題均為實數。
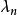斯圖姆與利烏維爾變換2、對應於斯圖姆-利烏維爾問題的每一個特徵值 來說，有且僅有一個線性無關的特徵函式。
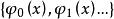斯圖姆與利烏維爾變換3、斯圖姆-利烏維爾問題的特徵函式系 滿足關係式
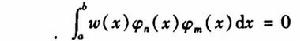斯圖姆與利烏維爾變換
斯圖姆與利烏維爾變換其中 。
