例如下函式中各行頻度n的計算:
for(i=0;i<n;i++) ----------------------------- (1)
{
for(j=0;j<n;j++) ------------------------- (2)
{
c[i][j]=0; ------------------------------ (3)
for(k=0;k<n;k++) ------------------- (4)
c[i][j]=c[i][j]+a[i][k]*b[k][j]; ------- (5)
}
}
(1.) for(i=0;i<n;i++) 頻度為: n+1
(2.) for(j=0;j<n;j++) n*(n+1)
(3.) c[i][j]=0 n*n
(4.) for(k=0;k<n;k++) n*n*(n+1)
(5.) c[i][j]=c[i][j]+a[i][k]*b[k][j] n*n*n
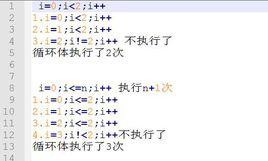
解釋:(1)i 變數在第一個 for 循環中,從取 i = 0 開始執行,直到i=n-1時為止,至此,i 執行了n次。加上最後i=n跳出循環的判斷,故,頻度共n+1 次;
(2). 與(1)不同,當 i 在 0~(n-1) 範圍內,內層循環[即是(2)的for循環]頻度為 n ; 當 i = n 時,內層循環語句沒執行。所以相當此時第(1)中 for 循環執行了n次,第二個for 循環執行了n次,加上最後j=n跳出循環的判斷,即,頻度共 n * (n+1);
(3). 此句語句,是要利用(1)、(2)for循環語句的i ,j 對 c[i][j] 進行賦值,此時,i 得到的賦值只有從 0 到 n -1, j 得到的賦值也是從0到n-1 ,都是 n次,此時(當 i 達到n-1 .\當 j 達到 n-1.)的 i++ \j++都不會執行。 故,頻度共 n*n 次;
(4). 同上(1),(2)的理由,單獨的(4)的for 循環執行了n+1 次,綜上,頻度為 n*n*(n+1);
(5). 同理(3),對於三個for 循環, i 得到的賦值只有從 0 到 n , j 得到的賦值也是從0到n ,k得到的賦值也是從 0 到 n ,即,頻度為n*n*n。