概念
所謂整數劃分,是指把一個正整數n寫成為
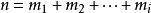 整數劃分
整數劃分 整數劃分
整數劃分 整數劃分
整數劃分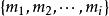 整數劃分
整數劃分其中, 為正整數,並且 ; 為n的一個劃分。
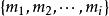 整數劃分
整數劃分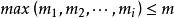 整數劃分
整數劃分如果 中的最大值不超過m,即 ,則稱它屬於n的一個m劃分。
求劃分個數
分析
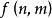 整數劃分
整數劃分這裡我們記n的m劃分的個數為 。
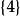 整數劃分
整數劃分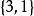 整數劃分
整數劃分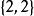 整數劃分
整數劃分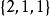 整數劃分
整數劃分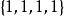 整數劃分
整數劃分例如,當n=4時,有5個劃分,即 , , , , 。
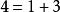 整數劃分
整數劃分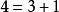 整數劃分
整數劃分注意: 和 被認為是同一個劃分。
根據n和m的關係,考慮一下幾種情況:
 整數劃分
整數劃分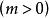 整數劃分
整數劃分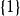 整數劃分
整數劃分(一)當 時,無論m的值為多少 ,只有一種劃分,即 。
 整數劃分
整數劃分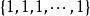 整數劃分
整數劃分(二)當 時,無論n的值為多少,只有一種劃分,即n個1, 。
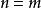 整數劃分
整數劃分(三)當 時,根據劃分中是否包含n,可以分為以下兩種情況:
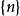 整數劃分
整數劃分(1)劃分中包含n的情況,只有一個,即 。
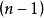 整數劃分
整數劃分(2)劃分中不包含n的情況,這時劃分中最大的數字也一定比n小,即n的所有 劃分。
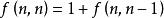 整數劃分
整數劃分因此 。
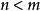 整數劃分
整數劃分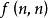 整數劃分
整數劃分(四)當 時,由於劃分中不可能出現負數,因此就相當於 。
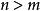 整數劃分
整數劃分(五)當 時,根據劃分中是否包含最大值m,可以分為以下兩種情況:
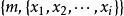 整數劃分
整數劃分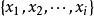 整數劃分
整數劃分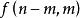 整數劃分
整數劃分(1)劃分中包含m的情況,即 ,其中 的和為n-m,因此這種情況下為 。
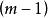 整數劃分
整數劃分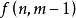 整數劃分
整數劃分(2)劃分中不包含m的情況,則劃分中所有值都比m小,即n的 劃分,個數為 。
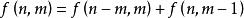 整數劃分
整數劃分因此 。
綜上所述:
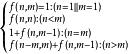 整數劃分
整數劃分JAVA實現
利用計算機計算(C語言)
求具體劃分集合
分析
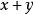 整數劃分
整數劃分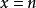 整數劃分
整數劃分 整數劃分
整數劃分 整數劃分
整數劃分把一個正整數n分成 ,若使 ,可求出一種劃分,再使x遞減,令x是劃分好的數,按此方法繼續對y繼續進行分解,以此類推,直到 (不包含 )為止,這樣就求出了所有劃分。
在分解時應保證分解數x有序,即上一次的x要大於等於這一次的x,以避免求出元素相同但位置不同的結果。
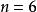 整數劃分
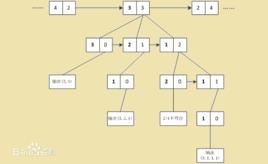
整數劃分例:當 時,部分過程如下圖所示:
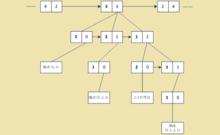 當n=6時的部分過程
當n=6時的部分過程