定義
摺紙數理學指的是對摺紙藝術從數學的角度加以研究。例如，研究某個特定的紙模型的可展性以及使用摺紙來解數學方程。
某些經典幾何作圖問題，例如：三等分角，或者將立方體的體積擴大一倍（倍立方）等問題都被證明為尺規作圖不可能解決的。但是它們可以通過幾個摺紙步驟加以解決。一般地，摺紙可以通過作圖求解不超過4次的代數方程。Huzita-Hatori 公理集是這一領域的重要研究成果。
相關理論
芳賀定理
（賀芳和夫提出） ：
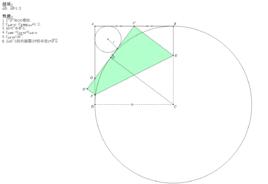
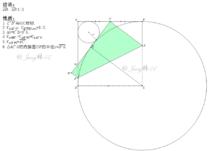
摺紙幾何學芳賀第一定理
-芳賀第一定理
結論：GD：AD=1:3
套用：1.折分數
2.折任意精度的整數度角
-芳賀第二定理
-芳賀第三定理
折取正多邊形
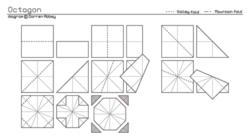在正方形中折取正多邊形正三角形
正五邊形
正六邊形
正七邊形
正八邊形
歷史
19世紀末，摺紙在西方成為了數學和科學研究的工具。
20世紀70年代，日本學者將目光投向摺紙中的數理，之後在日本形成了一個研究摺紙數理的高潮，結成了多個研究團體，也出版了許多的專著 ，芳賀和夫、阿部恆、堀井洋子、布施知子、笠原邦彥、前川淳等學者作出了較大的貢獻。
進入90年代，在世界上許多國家掀起一股熱潮。
1989年，第一屆摺紙科學國際會議在義大利的費拉拉城召開。
1994年，第二屆摺紙科學國際會議上，日本學者芳賀和夫提議，在origami的詞未加上後綴-cs，用來表示正在形成的用摺紙來探究數理的一門新學問
學科特性
1.題材的活動性
2.結果的意外性
3.結論的有用性
4.課題的發展性
5.內容的趣味性
6.問題的挑戰性
7.學科的成長性
教育意義
1.新的學習方式的推廣
2.數學學習興趣的激發
3.數學思想方法及科學方法的養成
4.空間想像能力的培養
5.探索與創新能力的培養
出版物
1896年，桑達拉《摺紙中的幾何練習》，研究摺紙數理學的第一本專著
1924年，拉波《摺紙的操作》出版
1935~1936年，貝洛柯發表了論文《用摺紙解幾何問題》和《用摺紙解3次和4次方程》
20世紀70年代，伏見康治夫婦的著作《摺紙幾何學》
