概述
理論由來
1776年法國科學家庫倫(C.A.Coulomb)總結土的破壞現象和影響因素,提出土的破壞公式為:
根據砂土試驗結果得到:
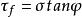 摩爾-庫侖理論
摩爾-庫侖理論對於粘性土,可給出更為普遍的表達式:
 摩爾-庫侖理論
摩爾-庫侖理論摩爾(Mohr)繼續庫倫的早期研究工作,提出材料的破壞是剪下破壞的理論,認為在破裂面上,法向
 摩爾-庫侖理論
摩爾-庫侖理論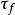 摩爾-庫侖理論
摩爾-庫侖理論應力 與抗剪強度 之間存在著函式關係,即:
 摩爾-庫侖理論
摩爾-庫侖理論這種以庫倫公式作為抗剪強度公式,根據剪應力是否達到抗剪強度作為破壞標準的理論就是摩爾-庫倫
理論。
理論介紹
當土體中任一平面上的某點剪應力等於土的抗剪強度時,該點即處於瀕於破壞的臨界狀態,此臨界狀態即稱為"極限平衡狀態”。該狀態下各種應力之間的關係稱為"極限平衡條件”。
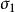 摩爾-庫侖理論
摩爾-庫侖理論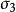 摩爾-庫侖理論
摩爾-庫侖理論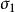 摩爾-庫侖理論
摩爾-庫侖理論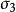 摩爾-庫侖理論
摩爾-庫侖理論 摩爾-庫侖理論
摩爾-庫侖理論 摩爾-庫侖理論
摩爾-庫侖理論由“土中應力分布”可求得在自重和豎向附加應力作用下土體中任一點M的應力狀態 和 [圖5-3(a)]。為簡單起見,以平面應變課題為例,研究該點是否產生破壞。如圖5-3(b)所示,該點土單元體兩個相互垂直的面上分別作用著最大主應力 和最小主應力 。若忽略其自身重力,則根據靜力平衡條件,可求得任一截面m-n上的法向應力 和剪應力 為
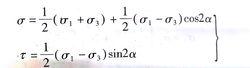 摩爾-庫侖理論
摩爾-庫侖理論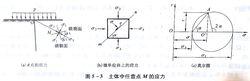 摩爾-庫侖理論
摩爾-庫侖理論 摩爾-庫侖理論
摩爾-庫侖理論 摩爾-庫侖理論
摩爾-庫侖理論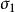 摩爾-庫侖理論
摩爾-庫侖理論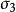 摩爾-庫侖理論
摩爾-庫侖理論由材料力學應力狀態分析可知,以上 , 與 , 的關係也可用莫爾應力圓表示[圖5-3(c)]。其圓固各點的坐標即表示該點在相應平面上的法向應力和剪應力。
 摩爾-庫侖理論
摩爾-庫侖理論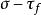 摩爾-庫侖理論
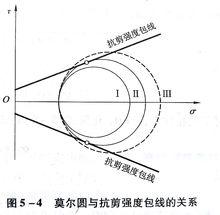
摩爾-庫侖理論為判別M點土是否被破壞,可將該點的莫爾應力圓與土的抗剪強度包線 繪在同一坐標圖上並作相對位置比較。如圖5-4所下,它們之間的關係存在以下三種情況
(1)M點莫爾應力圖整體位於杭剪強度包線的下方(圓1),莫爾應力圓與抗剪強度線相離,表明該點在任何平面上的剪應力均小於土所能發揮的抗剪強度,表明該點未被剪破。
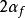 摩爾-庫侖理論
摩爾-庫侖理論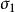 摩爾-庫侖理論
摩爾-庫侖理論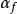 摩爾-庫侖理論
摩爾-庫侖理論(2)M點莫爾應力圓與杭剪強度包線相切(圓2),說明在切點所代表的平面上,剪應力恰好等於土的抗剪強度,該點就處於極限平衡狀態,此時莫爾應力圓亦稱極限應力圓,由圖中切點的位置還可確定M點破壞面的方向。連線切點與莫爾應力圓圓心,連線與橫坐標之間的夾角為 ,根據莫爾圓原理,可知土體中M點的破壞面與最大主應力 作用面方向夾角為 [圖5-5(a)]。
(3)M點莫爾應力圓與杭剪強度包線相割(圓3),則M點早已破壞,應力已超出彈性範疇,圓3所代表的應力狀態是不可能存在的。
上體處於極限平衡狀態時,從圖5-5(a)中莫爾圓與抗剪強度包線的幾何關係可推得黏性上的極限平衡條件為
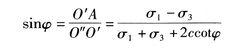 摩爾-庫侖理論
摩爾-庫侖理論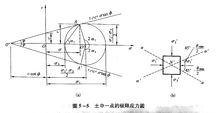 摩爾-庫侖理論
摩爾-庫侖理論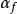 摩爾-庫侖理論
摩爾-庫侖理論根據圖5-5中幾何關係,可得破壞面與最大主應力作用面間的夾角為
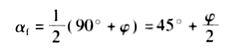 摩爾-庫侖理論
摩爾-庫侖理論 摩爾-庫侖理論
摩爾-庫侖理論 摩爾-庫侖理論
摩爾-庫侖理論在極限平衡狀態時,由圖5一3(a)中看出:通過M點將產生一對破裂面,它們均與最大主應力作用面成
夾角,相應地在莫爾應力圓上橫坐標上下對稱地有兩個破裂面a一a和a'一a'[圖5-5b)],而這一對破裂面之間在最大主應力作用方向的夾角為90度-。