定義
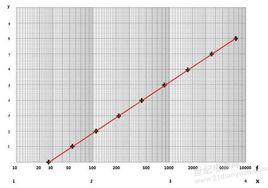
圖1 指數方程指數方程(exponential equation)是在指數里含有未知數的方程叫做指數方程。
反函式
對數方程：在對數符號後面含有未知數的方程。
基本思想
化同底或換元。
例題
方程(1/2)^x=x,x的解為
a.(1/10,1/5)
b.(3/10,2/5)
c.(1/2,7/10)
d.(9/10,1)
解這種題目有兩種方法。一、二分法求方程的解。把方程變形得到：(1/2)^x-x=0，設函式Y=(1/2)^x-x，那么解這個方程也就是要求Y=0的時候X的值，也就是求函式Y=(1/2)^x-x與X軸交點的橫坐標，畫圖後可以看出只有一個解。那么假設這個解為A，那么對於大於A的數M和小於A的數N，必定有f(M)*f(N)<0,仔細想想，點（A，0）在X軸上，它兩邊的函式一邊大於0，一邊小於0。隨便帶如果兩個比較簡單的數，求函式值，如果一正一負，那么f(M)*f(N)<0，A就必定在（M，N）區間內，取M和N的中點，算函式值，看這個函式值是大於0還是小於0，再與N或M組成一個區間，A必定在這個區間內，再重複這種操作，就可以求出解的很精確的數值。二、這是選擇題，把答案帶如檢驗也可以。分別把四個選項的兩個數帶如上述函式，看其乘積是否小於0，如果是，根就在這個區間內。檢驗之後，只有C符合。所以選C。
解題關鍵
如何將指數方程化歸為一元一次、一元二次方程。在化歸過程中有時兩邊化同底，有時兩邊取對數，有時恰當變形後換元，充分體現了化歸思想和熟悉化解題原則。
解法
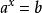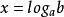指數方程
指數方程（1）方程的解法：形如 的方程，方程的解是 。
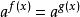指數方程（2）方程的解法：形如 的方程，將方程化為f(x)=g(x)。
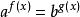指數方程（3）方程的解法：形如 的方程，將方程化為f(x)lga=g(x)lgb。
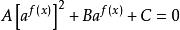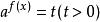指數方程
指數方程（4）方程的解法： 形如 的方程，設 方程可化為At2+Bt+C=0。
對比
對數方程：在對數符號後面含有未知數的方程。
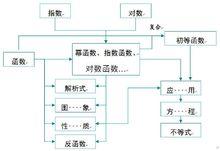圖2 指數與對數對比圖冪函式：指數為常數，底數含有未知數的方程。
套用——解Burgers-BBM方程
根據非線性Burgers-BBM方程的特點,利用指數函式展開法及齊次平衡原理,通過一個變換技巧,並藉助Maple數學軟體強大符號運算功能,簡捷地獲得了Burgers-BBM方程的行波解、孤立波解及三角函式周期解.並用Maple軟體獲得3個典型的波形圖。
