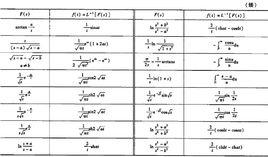
主要形式
1、對數與指數的變換
為求乘積ab
可先取對數 ln(ab)= lna+lnb
再取指數運算
2、相量與正弦量的變換
為了計算正弦穩態回響,可將激勵源變為相量,然後在頻率域裡求相量(即相量法),然後再變回時域得到正弦時間函式回響。
其中 此複數的模 就是正弦量u(t)的振幅值,幅角就是u(t)的初相角。這種對應關係就是一種變換。
定義
定義式:設有一時間函式f(t) [0,∞] 或 0≤t≤∞單邊函式
其中,S=σ+jω 是復參變數,稱為復頻率。
左端的定積分稱為拉普拉斯積分,又稱為f(t)的拉普拉斯變換;
右端的F(S)是拉普拉斯積分的結果,此積分把時域中的單邊函式f(t)變換為以復頻率S為自變數的復頻域函式F(S),稱為f(t)的拉普拉斯象函式。
以上的拉普拉斯變換是對單邊函式的拉普拉斯變換,稱為單邊拉普拉斯變換。
如f(t)是定義在整個時間軸上的函式,可將其乘以單位階躍函式,即變為f(t)ε(t),則拉普拉斯變換為
其中積分下標取0-而不是0或0+ ,是為了將衝激函式δ(t)及其導函式納入拉普拉斯變換的範圍。
這是複變函數的積分
拉氏變換和拉氏反變換可簡記如下
F(S)=L[f(t)] ; f(t)=L-1[F(s)]
當 >0時,結果為有限值即
具體的說,即Re[s]- Re[a]=σ- Re[a] > 0 有σ> Re[a]這時eatε(t)的拉氏變換存在。我們稱σ> Re[a]的s=σ+jω的範圍為該函式的拉氏變換的收斂域,一般而言,對一個具體的單邊函式f(t),並非所有的σ值都能使f(t)eσt絕對可積,即把能使用f(t)eσt絕對可積的s的範圍稱為單邊函式f(t)的拉氏變換的收斂域。
收斂域可以在s平面上表示出來
假定以下需進行拉氏變換的函式,其拉氏變換都存在
1、線性組合定理
L[af1(t)±bf2(t)]=aL[f1(t)]±b[f2(t)]
若干個原函式的線性組合的象函式,等於各個原函式的象函式的線性組合
套用
套用拉普拉斯變換解常變數齊次微分方程,可以將微分方程化為代數方程,使問題得以解決。在工程學上,拉普拉斯變換的重大意義在於:將一個信號從時域上,轉換為復頻域(s域)上來表示,對於分析系統特性,系統穩定有著重大意義;線上性系統,控制自動化上都有廣泛的套用。
相關條目
z轉換
微分方程
線性系統
傅立葉變換
信號處理
Laplacian運算元