萬有引力定律的驗證
英國科學怪傑卡文迪許於1789年用他發明的扭秤,驗證了牛頓的萬有引力定律的正確性,並測出了引力常量,卡文迪許的實驗結果跟現代測量結果是很接近的,它使得萬有引力定律有了真正的實用價值,卡文迪許也被人們稱為第一個“能稱出地球質量的人”。
 扭秤實驗
扭秤實驗牛頓的另一偉大貢獻是他的萬有引力定律,但是萬有引力到底多大?
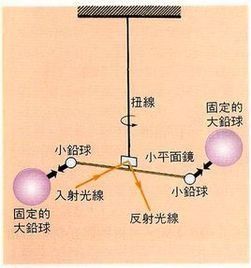
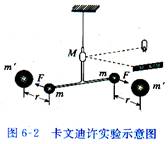
18世紀末,英國科學家亨利·卡文迪許決定要找出這個引力。他將小金屬球系在長為6英尺(1英尺等於0.3048米)木棒的兩邊並用金屬線懸吊起來,這個木棒就像啞鈴一樣。再將兩個350磅(1磅等於0.4536千克)的銅球放在相當近的地方,以產生足夠的引力讓啞鈴轉動,並扭轉金屬線。然後用自製的儀器測量出微小的轉動。測量結果驚人地準確,他測出了萬有引力恆量的參數,萬有引力常量約為G=6.67259x10^-11 (N·m^2 /kg^2)通常取G=6.67×10^-11(N·m^2/kg^2),在此基礎上卡文迪什計算地球的密度和質量。卡文迪什的計算結果是地球的質量為6.0 x10^24kg。
庫侖定律的驗證
法國物理學家庫侖於1785年利用他發明的扭秤實驗,測定了電荷之間的作用力。庫侖在實驗中發現靜電力與距離平方成反比,同時他也認識到了靜電力與電量的乘積成正比,從而得到了完整的庫侖定律。庫侖定律第一次打開了電的數學理論的大門,使靜電學進入了定量研究的新階段,也為泊松等人發展電學理論奠定了基礎。庫侖還曾用扭秤證明了地磁場對磁針有力矩的作用,力矩大小與磁針對子午線偏斜角的正弦成正比,這構成了磁矩概念的基礎。
庫侖定律是一有關基本力的的定律,它的指數是否精確為2,關係到高斯定理是否正確,因此兩百多年來,它的正確性不斷經歷著實驗的考驗。
庫倫曾用扭秤裝置做過大量實驗工作,但值得注意的是,在精度方面遠不如萬有引力定律的扭秤實驗。試驗中的帶電小球都是有限大的帶電體,兩帶電體之間的距離不可能很大,,因此將兩帶電小球視為點電荷就不夠精確,同時兩球上的電荷分布互有影響,特別是兩帶電球之間的距離也無法精確測定,而且還存在漏電現象。因此設分母中r的指數為2+δ,庫倫本人的實驗誤差是δ≤0.04,即庫侖定律表示為F=[k*q(1)*q(2)]/r^(2±0.04)。英國科學家卡文迪許於1773年測得δ≤0.02。
後人曾改進實驗裝置來驗證庫侖定律。
由於萬有引力定律於庫侖定律之間的相似性,扭秤實驗不失為一種同用的方法。