理論基礎
A. 光的雙折射效應
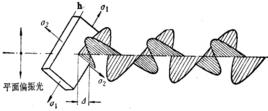
晶體光學指出,對於內部原子有序排列、具有各向異性的晶體材料(如石英,方解石、雲母、金剛石等)而言,光在其中沿各個方向的折射率不同,因而傳播速度不同,由此導致一束光入射這種晶體後出現兩束折射光。在一定條件下,兩束光會在介質中發生干涉現象,產生可見的干涉條紋,這就是光的雙折射效應。
B. 暫時(人工)雙折射
玻璃、塑膠、環氧樹脂等各向同性透明非晶體材料,自然狀態下通常不產生雙折射現象,但當有載荷作用時,其內部會產生應力分布,導致材料由原先的光學各向同性變為各向異性,出現類似晶體的雙折射性質,光沿著主應力σ及σ方向分解成兩束平面偏振光,其振動方向互相垂直,且傳播速度不同,當載荷卸去後,雙折射現象也即消失,這種現象稱為暫時(人工)雙折射。
發展
實驗定律
1854年,法國實驗固體物理學家維爾泰姆首先在實驗中發現並總結出了應力-光學定律,建立起了彈性雙折射效應中應力與折射率的關係彈性雙折射效應中應力與折射率的關係。
理論證明
由材料力學應力分析知識可知,材料中主應力和主應變的方向是一致的.我們有理由作出如下推論:由應力導致具有各向異性的材料內部的折射率主軸與應力或應變的主軸方向是一致的,即二者共軸.事實上這個結論已通過實驗證明。
根據應力狀態分析理論,材料中一點所在應力單元體的應力狀態在數學上一般可以用一個二次曲面方程表達
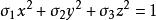 應力-光學定律
應力-光學定律其中σ,σ,σ是沿x,y,z軸方向的主應力,當σ,σ,σ三者同號時,二次曲面為一橢球面,稱之為應力橢球。各向異性材料折射率橢球方程為
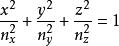 應力-光學定律
應力-光學定律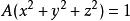 應力-光學定律
應力-光學定律由推論可得,應力橢球與折射率橢球在應力作用下是共軸的,所以其圓形中心截面(即橢球與其同心球交線所在的平面)相互平行.現考慮兩橢球與其同心球 的交線,聯立可得
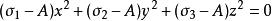 應力-光學定律
應力-光學定律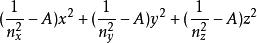 應力-光學定律
應力-光學定律因為兩平面相互平行,所以方程係數滿足
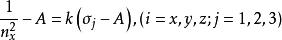 應力-光學定律
應力-光學定律故可得1/n與σ 存在一階線性關係
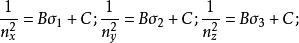 應力-光學定律
應力-光學定律對於沿任一給定方向S(Sx,Sy,Sz)將其單位矢量代入兩橢球方程,並聯立上式進一步推導可得,該方向折射率n與應力σ均滿足線性關係
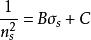 應力-光學定律
應力-光學定律設材料在無應力作用時的初始折射率為n,現將常數C表示成如下形式:
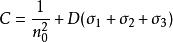 應力-光學定律
應力-光學定律代入上上式得
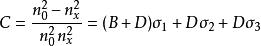 應力-光學定律
應力-光學定律因為n-n、n、n,所以
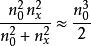 應力-光學定律
應力-光學定律再令
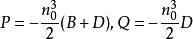 應力-光學定律
應力-光學定律代入上式可得
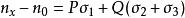 應力-光學定律
應力-光學定律同理可得
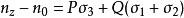 應力-光學定律
應力-光學定律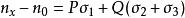 應力-光學定律
應力-光學定律式中P稱為縱向應力光學常數,Q稱為橫向應力光學常數,其數值取決於應力作用材料本身的性質。
聯立得:
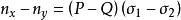 應力-光學定律
應力-光學定律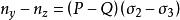 應力-光學定律
應力-光學定律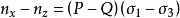 應力-光學定律
應力-光學定律這就是維爾泰姆應力-光學定律。
套用
應力-光學定律是光彈性法的理論基礎。
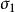 應力-光學定律
應力-光學定律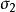 應力-光學定律
應力-光學定律在偏振光場中,各向同性的光彈性模型在載荷作用下會產生暫時雙折射效應,其主折射率和主應力有關,主折射率又可由相應的光程差來確定,因此可用光程差來確定主應力。一束自然光通過起偏鏡後,會產生平面偏振光。它垂直透射一個受載荷的平面模型時,沿著模型的一點的兩個主應力和的方向分解成兩束速度不同的平面偏振光,它們通過模型後,產生一個相對光程差⊿。實驗表明,模型的主應力和與光程差⊿之間的關係如下:
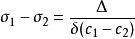 應力-光學定律
應力-光學定律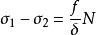 應力-光學定律
應力-光學定律即 ,
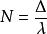 應力-光學定律
應力-光學定律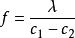 應力-光學定律
應力-光學定律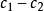 應力-光學定律
應力-光學定律式中為等差線(又稱等色線)條紋級數;為光彈性材料條紋值;δ為光彈性模型的厚度;λ為光源的波長;()為應力光學常數。
上式是著名的應力-光學定律,它是光彈性法的理論基礎。