應力雙折射
常以折射率橢球方程描述晶體的光學特性。在主軸坐標系中,折射率橢球方程可以寫為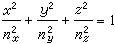 。 (1)
。 (1)
a1x2+a2y2+a3z2+a4yz+a5xz+a6xy=1。 (2)
式(2)與式(1)相比各項係數之差與各應力分量成正比,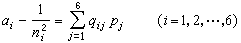 , (3)
, (3)
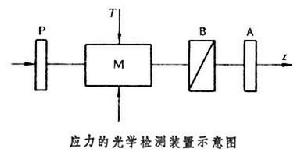
各向同性材料,情況要簡單得多。若將受力T作用的各向同性材料M放在兩正交偏振器P與A之間(如圖),取光傳播方向為z軸,材料在z軸方向長度為l,力與z軸垂直。光通過M後,兩偏振分量的位相差近似為
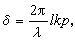 (4)
(4)
 應力雙折射
應力雙折射
應力雙折射指透明的固體媒質在壓力或張力的作用下,折射率特性會發生改變。若媒質是光學各向同性的,那么外力的作用就使它成了各向異性的,會產生雙折射。若媒質本來就是光學各向異性的晶體,那么外力作用會使它產生一個附加的雙折射,這一現象稱為應力雙折射,也稱為機械雙折射或光測彈性效應。T.J.塞貝克在1813年和D.布儒斯特在1816年最早研究了這一現象。
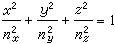 。 (1)
。 (1)
a1x2+a2y2+a3z2+a4yz+a5xz+a6xy=1。 (2)
式(2)與式(1)相比各項係數之差與各應力分量成正比,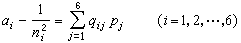 , (3)
, (3)
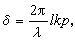 (4)
(4)
 應力雙折射
應力雙折射