定義
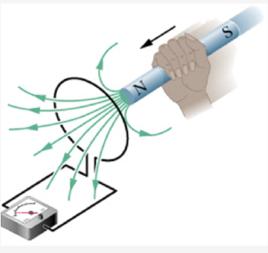
變化的磁場在其周圍空間激發感生電場(又稱有鏇電場),這種感生電場迫使導體內的電荷作定向移動而形成感生電動勢。 如圖式子中E鏇是有鏇電場的場強,即單位正電荷所受有鏇電場的作用力。
感生電場在閉合導體迴路L中產生感生電動勢:
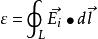 感生電動勢
感生電動勢感生電場在一段導體ab兩端上的感生電動勢:
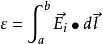 感生電動勢
感生電動勢 感生電動勢
感生電動勢 感生電動勢
感生電動勢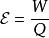 感生電動勢
感生電動勢假設,電荷 移動經過一個電動勢源後,獲得了能量 ,則此元件的電動勢定義為 。通常,這能量是分離正負電荷所做的功,由於這正負電荷被分離至元件的兩端,會出現對應電場與電壓差。
在電磁學裡,電動勢又分為兩種:“感生電動勢”與“動生電動勢”。根據法拉第感應定律,處於含時磁場的閉電路,由於磁場隨著時間而改變,會有感生電動勢出現於閉電路。感生電動勢等於電場沿著閉電路的路徑積分。處於閉電路的帶電粒子會感受到電場,因而產生電流。
移動於磁場的細直導線,其內部會出現動生電動勢。處於這導線的電荷,根據洛倫茲力定律,會感受到洛倫茲力,從而造成正負電荷分離至直棍的兩端。這動作會形成一個電場與伴隨的電場力,抗拒洛倫茲力,直到兩種作用力達成平衡。
歷史
從1825年到1826年之間,格奧爾格·歐姆做了很多有關於電路的實驗。1827年,在他發表的書《直流電路的數學研究》( Die galvanische Kette, mathematisch bearbeitet)裡面,論述了很多這些實驗和從這些實驗中得到的結果,包括著名的“歐姆定律”。歐姆注意到電路所需要的電源是由電池供給的,電池與電路內的各種物理現象應該有密切關係。他推論電池具有某種“驅動力”,能夠驅使電流流動於電路。他將幾個伏打電池串聯在一起,發覺電流與伏打電池的數量成正比。因此,他提出驅動力與電流成正比。這驅動力就是我們所知的電動勢,在一個簡單的電阻電路里,電動勢等於電流乘以電阻。
後來,於1831年,麥可·法拉第做了一系列有關電磁感應的實驗,從這些實驗,他發現以下幾點:
當改變載流導線的電流時,附近的閉電路會被感應出電流。
當移動磁鐵時,附近的閉電路會被感應出電流。
當移動閉電路於載流導線或磁鐵附近時,這閉電路會被感應出電流。
1.當改變載流導線的電流時,附近的閉電路會被感應出電流。
2.當移動磁鐵時,附近的閉電路會被感應出電流。
3.當移動閉電路於載流導線或磁鐵附近時,這閉電路會被感應出電流。
於1832年,法拉第又發現,產生於不同導線的感應電流與導線的電導率成正比。由於電導率與電阻成反比,這顯示出感應作用涉及了電動勢,感應電流是由電動勢驅使導線的電荷移動而形成的;而且,不論導線是開電路,或是閉電路,都會感應出電動勢。
成因
麥克斯韋提出:變化的磁場在其周圍空間激發一種新的電場,稱為感生電場或渦鏇電場。處於電場的中的電荷會受到感生電場力的作用,感生電場力是產生電動勢的非靜電力,其感應電場的存在與是否存在閉合電路無關。
 感生電動勢
感生電動勢變化的磁場周圍所產生的電場與電荷周圍的靜電場的區別:
a.靜電場由電荷激發,而磁場周圍的電場是由變化的磁場激發的。
b.靜電場的電場線不閉合,總是出發於正電荷,終止於負電荷,且單位正電荷在電場中沿閉合電路運動一周時,電場力所做的功為零。而變化的磁場周圍的電場中的電場線是閉合曲線,沒有終點與起點,這種情況與磁場中的磁感線類似,所以,單位正電荷在此電場中沿閉合電路運動一周時,電場力所做的功不為零。
應該指出,按照引起磁通量變化原因的不同,把感應電動勢區分為動生電動勢和感生電動勢。感生電動勢和動生電動勢根本區別在於磁場是否變化,磁場不變則產生的電動勢是動生電動勢。磁場變化產生的電動勢是感生電動勢。當然,可以感生電動勢和動生電動勢同時產生。因此,磁棒插入線圈,不論以誰作為參考系,都是感生電動勢,不能因為磁棒運動了就說是動生電動勢,因為此時電動勢成因並不是因為洛倫茲力。
定律
法拉第電磁感應定律
表達式如下:
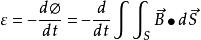 感生電動勢
感生電動勢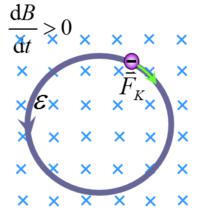 感生電動勢
感生電動勢當閉合迴路不動而穿過閉合迴路的磁場變化時
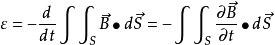 感生電動勢
感生電動勢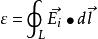 感生電動勢
感生電動勢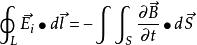 感生電動勢
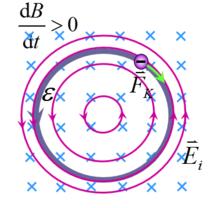
感生電動勢變化的磁場產生感生電場
 感生電動勢
感生電動勢麥克斯韋從物理內涵上闡述了出現感應電動勢的本質是產生了感生電場;
產生感生電動勢的非靜電力就是感生電場作用在電荷上的力——感生電場力
計算
感生電動勢的計算
方法一:
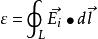 感生電動勢
感生電動勢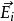 感生電動勢
感生電動勢這種方法要求先計算出積分路徑上各點的 ,再通過對做積分得到感生電動勢 ;
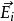 感生電動勢
感生電動勢但是在一般情況下,計算 是困難的,所以只有在某些對稱情況下(如長螺線管形成的變化磁場區域),才能比較方便計算感生電動勢。
方法二:
套用電磁感應定律計算
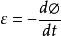 感生電動勢
感生電動勢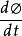 感生電動勢
感生電動勢對於閉合電路,只需知道線圈的 ,就可求出感生電動勢;
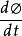 感生電動勢
感生電動勢對於非閉合的一段導線ab,可假設一條輔助曲線與ab組成閉合迴路,只要知道這個閉合迴路的 也可以用法拉第定律求出感生電動勢。