定義
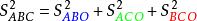 德古阿定理
德古阿定理 若從一個正六面體截下一角O形成一截角錐(記為ABCO),則
勾股定理
勾股定理又稱商高定理、畢達哥拉斯定理、畢氏定理、百牛定理,是平面幾何中一個基本而重要的定理。勾股定理說明,平面上的直角三角形的兩條直角邊的長度(古稱勾長、股長)的平方和等於斜邊長(古稱弦長)的平方。反之,若平面上三角形中兩邊長的平方和等於第三邊邊長的平方,則它是直角三角形(直角所對的邊是第三邊)。
勾股定理是人類早期發現並證明的重要數學定理之一。
據《周髀算經》中記述,公元前一千多年周公與商高論數的對話中,商高就以三四五3個特定數為例詳細解釋了勾股定理要素,其一,“以為句廣三,股修四,徑隅五”。其二,“既方其外,半之一矩,環而共盤,得成三四五。兩矩共長二十有五,是謂積矩。”首先肯定一個底寬為三,高為四的直角三角形,弦長必定是五。最重要的是緊接著論證了弦長平方必定是兩直角邊的平方和,確立了直角三角形兩條直角邊的平方和等於斜邊平方的判定原則。其判定方法後世不明其法而被忽略。
此外,《周髀算經》中明確記載了周公後人陳子敘述的勾股定理公式:“若求邪至日者,以日下為勾,日高為股,勾股各自乘,並而開方除之,得邪至日”。
趙爽在《周髀算經注》中將勾股定理表述為“勾股各自乘,並之,為弦實。開方除之,即弦 ”。
古埃及在公元前2600年的紙莎草就有(3,4,5)這一組勾股數,而古巴比倫泥板涉及的最大的一個勾股數組是(12709,13500,18541)。
有些參考資料提到法國和比利時將勾股定理稱為驢橋定理,但驢橋定理就是等邊對等角,是指等腰三角形的二底角相等,非勾股定理。
即在平面上的一個直角三角形中,兩個直角邊邊長的平方加起來等於斜邊長的平方。如果設直角三角形的兩條直角邊長度分別是a和b,斜邊長度是c,那么可以用數學語言表達:
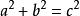 德古阿定理
德古阿定理 餘弦定理是勾股定理的一個推廣。勾股定理現約有400種證明方法,是數學定理中證明方法最多的定理之一。