基本概念
復點,復直線 以複數為坐標的點或直線稱為復點或復直線。
復元素 復點和復直線統稱復元素。
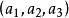 復點
復點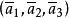 復點
復點共軛復元素 若為一元素的齊次坐標時,為另一同類元素的齊次坐標,則此二元素叫做共軛復元素。
兩個非無窮遠共軛復元素,其非齊次坐標必為共軛複數。
兩個共軛復元素的齊次坐標不一定為共軛複數,原因是齊次坐標可以相差一個常數因子 。
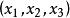 復點
復點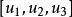 復點
復點復點和復直線的結合關係為
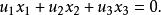 復點
復點相關定理
定理1 一元素為實元素的充要條件是該元素與其共軛復元素重合。
 復點
復點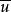 復點
復點定理2 如果一點x在一直線u上,則共軛復點必在共軛直線上。
定理3 兩共軛復直線的交點為一實點,兩共軛復點的連線為一實直線。
推論 在一復直線上有唯一一個實點,過一復點有唯一一條實直線。
注:一實直線上的點或為實點或為一共軛復點;過一實點的直線或為一實直線或為一-共軛復直線 。
例題選解
例1 證明:(2,i,1-i)與(2+2i,1-i,2i)表示一對共軛復點,並求其連線方程。
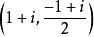 復點
復點證明: 點(2,i,1-i)之非齊次坐標為,
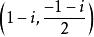 復點
復點點(2+2i,1-i,2i)之非齊次坐標為。
顯然其坐標為共軛複數,所以此二點為共軛復點,其連線方程為:
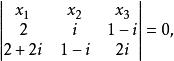 復點
復點即
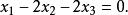 復點
復點例2 (1)求過(1,i,0)之實直線;
(2)求直線[2,i,3-4i)上之實點。
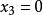 復點
復點解: (1)通過點(1,i,0)之實直線必過其共軛復點(1,-i,0),故所求為。
(2)直線[2,i,3-4i]上之實點為它與共軛復直線[2,-i,3+4i]之交點,故所求為點(-3,8,2) 。