概述
復立體是在廣義冪指函式角度下的複平面理論。
復立體定義
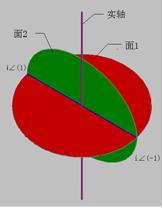 復立體附圖
復立體附圖如左圖所示,在三維空間中存在實軸。在實軸的原點處作垂面1定義為虛面。在虛面上作單位圓定義為虛圓。從虛圓圓上選取某特定的一個直徑和實軸組成面2定義為標準複平面。虛圓上其他直徑和實軸組成非標準複平面。
虛圓上的點即由-1所有二次方根組成。選定的直徑為i∠(0)和i∠(-1)(定義見後,前者即為i,後者即為-i)。
無論標準複平面還是非標準複平面,其面內皆可以進行加減等運算。同時,標準複平面就是現有的複平面,
目前的複平面理論皆適用。
任何復立體中的點,都可以用一個從原點出發的矢量(稱為復立體矢量)表示,這種矢量不同於(i,j,k)矢量。
這個時候,任何復立體中的點,都表示為a×1+b×ix。其中,b×ix為廣義虛數,ix形式為i∠(x)。
復立體討論
根據公式
w^z=exp(z*Lnw)
=exp{z*[i*(arg(w)+2kπ)+ln|w|]},得到:
i^i和(-i)^(-i)均為exp[(π/2)+2kπ]。
Exp[(π/2)+2kπ]是個多等式,起因是Lnw多值引起。但是,換個角度,也可以認為i值多值引起,即假定定義某個ix,是現有複數i的一個元素,對應於Exp{-[(π/2)+2kπ]}的某個k。不同的ix對應不同的k值。用i∠(x)括弧中的數字來區分各個解。由於π/2並非唯一候選值,故括弧中的數字為對應於π/2時候的k。
這樣,-1即有無窮二次方根。從上面的復立體角度看,就是這些根均位於同一個平面上。
意義
復立體推廣了複平面理論,並指出代數基本定理需要推廣。
