數學表達式
在一定的變形條件下，當受力物體內一點的應力偏張力的第二不變數達到某一定值時，該點就開始進入塑性狀態。即
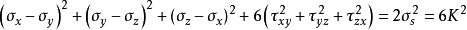廣義馮·米賽斯屈服準則用主應力表示為:
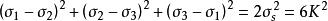廣義馮·米賽斯屈服準則式中
σ——材料的屈服點
K ——材料的剪下屈服強度
與等效應力比較，可得
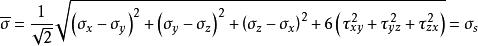廣義馮·米賽斯屈服準則所以，廣義馮·米賽斯屈服準則也可以表述為：在一定的變形條件下，當受力物體內一點的等效應力達到某一定值時，該點就開始進入塑性狀態。
米塞斯應力
在彈塑性有限元計算中，屈服準則的數學描述是整個計算的核心。因此有人將等效應力叫 做von Mises應力。因此大家在彈塑性力學的書里查不到von Mises應力的定義。這是有限元軟體里的一種叫法。它等同於等效應力，又稱應力強度。
stress intensity（應力強度），是由第三強度理論得到的當量應力，其值為第一主應力減去第三主應力。Von Mises是一種屈服準則,屈服準則的值我們通常叫等效應力。Ansys後處理中"Von Mises Stress"我們習慣稱Mises等效應力，它遵循材料力學第四強度理論(形狀改變比能理論)。
第三強度理論認為最大剪應力是引起流動破壞的主要原因，如低碳鋼拉伸時在與軸線成45度的截面上發生最大剪應力，材料沿著這個平面發生滑移，出現滑移線。這一理論比較好的解釋了塑性材料出現塑性變形的現象。形式簡單，但結果偏於安全。第四強度理論認為形狀改變比能是引起材料流動破壞的主要原因。結果更符合實際。
一般脆性材料，鑄鐵、石料、混凝土，多用第一強度理論。考察絕對值最大的主應力。
一般材料在外力作用下產生塑性變形，以流動形式破壞時，應該採用第三或第四強度理論。壓力容器上用第三強度理論（安全第一），其它多用第四強度理論。
第四強度理論應力，即mises（米塞斯）等效應力作為衡量應力水平的主要指標。mises應力是正應力和剪下應力的組合，常用來描繪聯合作用的複雜應力狀態。
mises stress的確是一種等效應力，它用應力等值線來表示模型內部的應力分布情況，它可以清晰描述出一種結果在整個模型中的變化，從而使分析人員可以快速的確定模型中的最危險區域。 它是根據第四強度理論計算的，因為它的計算公式是第四強度理論。
首先介紹一下形狀改變比能，然後看看強度條件的推導。
物體在外力作用下會發生變形，這裡所說的變形，既包括有體積改變也包括有形狀改變。當物體因外力作用而產生彈性變形時，外力在相應的位移上就作了功，同時在物體內部也就積蓄了能量。例如鐘錶的發條(彈性體)被用力擰緊(發生變形)，此外力所作的功就轉變為發條所積蓄的能。在放鬆過程中，發條靠它所積蓄的能使齒輪系統和指針持續轉動，這時發條又對外作了功。這種隨著彈性體發生變形而積蓄在其內部的能量稱為變形能。在單位變形體體積內所積蓄的變形能稱為變形比能。
由於物體在外力作用下所發生的彈性變形既包括物體的體積改變，也包括物體的形狀改變，所以可推斷，彈性體內所積蓄的變形比能也應該分成兩部分：一部分是形狀改變比能 ，一部分是體積改變比能。
物理意義
在一定的變形條件下，當材料的單位體積形狀改變的彈性位能（又稱彈性形變能）達到某一常數時，材料就屈服。
馮·米賽斯應力是基於剪下應變能的一種等效應力其值為：
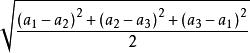廣義馮·米賽斯屈服準則其中a,a,a分別指第一、二、三主應力。
馮·米賽斯應力就是一種當量應力，它是根據第四強度理論得到的當量應力。 von mises stress 是綜合的概念，考慮了第一第二第三主應力，可以用來對疲勞，破壞等的評價。 YIELDING criterion （材料屈服標準）有基於stress analysis也有基於strain analysis的。 von mises stress（VMS）其實是一個STRESS yielding criterion.
我們認為對於某一材料來說，它都有一個yielding stress, 這個yielding stress 對應於相應的屈服點(yielding point)。
當材料受到外力刺激，如果其內部某處應力(VMS)大於這個yielding stress, 那么我們認為材料在此處有可能發生屈服。
Von Mises應力與Von MIses屈服準則，用在各向同性材料中較常見，來自於應力張量第一不變數。如果生物力學計算中缺乏材料數據，以近似材料參數代替，這種情況下似乎用VON應力也是可以的。
vms是材料力學中的第四屈服理論，主要是對塑性材料的，考慮的主要是疲勞效應。最大應力，最大應變主要是針對脆性材料的。
特點
廣義馮·米賽斯屈服準則具有如下優缺點:
優點：
（1）考慮了中主應力σ對屈服和破壞的影響；
（2）簡單實用，材料參數少，易於實驗測定；
（3）屈服曲面光滑，沒有稜角，利於塑性應變增量方向的確定和數值計算。
缺點：
（1）沒有考慮靜水壓力對屈服的影響；
（2）沒有考慮單純靜水壓力p對岩土類材料屈服的影響及屈服與破壞的非線性特性；
（3）沒有考慮岩土類材料在偏平面上拉壓強度不同的S-D效應，適用於金屬材料。
