提出背景
非參數回歸不需要模型滿足線性的假設前提,可以靈活地探測數據間的複雜關係,但是當模型中自變數數目較多時 ,模型的估計方差會加大,另外,基於核與光滑樣條估計的非參數回歸中自變數與因變數間關係的解釋也有難度,1985 年 Stone 提出加性模型 (additive models) ,模型中每一個加性項使用單個光滑函式來估計,在每一加性項中可以解釋因變數如何隨自變數變化而變化,很好地解決了上述問題 。 1990 年,Hastie 和 Tibshirani 擴展了加性模型的套用範圍 ,提出了廣義加性模型(generalized additive models)。
模型形式
 廣義加性模型
廣義加性模型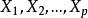 廣義加性模型
廣義加性模型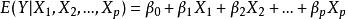 廣義加性模型
廣義加性模型經典的線性回歸模型假定因變數與自變數是線性形式:
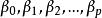 廣義加性模型
廣義加性模型其中,通過最小二乘法獲得。
加性模型擴展了線性模型:
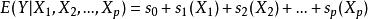 廣義加性模型
廣義加性模型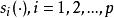 廣義加性模型
廣義加性模型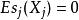 廣義加性模型
廣義加性模型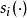 廣義加性模型
廣義加性模型其中,是光滑函式,,通過backfitting 算法 獲得。
廣義加性模型是廣義線性模型的擴展:
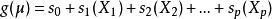 廣義加性模型
廣義加性模型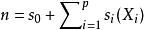 廣義加性模型
廣義加性模型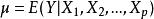 廣義加性模型
廣義加性模型 廣義加性模型
廣義加性模型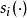 廣義加性模型
廣義加性模型其中,,為線性預測值,是非參數光滑函式 ,它可以是光滑樣條函式 、核函式或者局部回歸光滑函式 ,它的非參數形式使得模型非常靈活 ,揭示出自變數的非線性效應 。
 廣義加性模型
廣義加性模型 廣義加性模型
廣義加性模型 廣義加性模型
廣義加性模型 廣義加性模型
廣義加性模型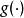 廣義加性模型
廣義加性模型 廣義加性模型
廣義加性模型模型不需要對的任何假設 ,由隨機部分 (random component) 、加性部分(additive component) 及聯結兩者的連線函式 (link function) 組成 ,反應變數的分布屬於指數分布族 ,可以是二項分布 、Poisson 分布 、Gamma 分布等。
模型中不必每一項都是非線性的 ,可以納入線性等參數項 ,因為每個解釋變數的關係如都用非參數擬合會出現計算量大 、過擬合等問題 ,有時因變數與某個預測變數的關係簡化成參數形式會更便於解釋 ,這樣就出現了半參數廣義加性模型 ( semi-parametric generalized additive models) ,其形式為 :
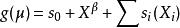 廣義加性模型
廣義加性模型優缺點
 廣義加性模型
廣義加性模型1) 可以引入非線性函式
 廣義加性模型
廣義加性模型 廣義加性模型
廣義加性模型2) 非線性可能使得對
預測的更準確3) 因為是”加性的”,所以,線性模型的假設檢驗的方法仍然可以使用
4) 因為是“加性”假設,所以GAMs中可能會缺失重要的互動作用,只能通過手動添加互動項來彌補
套用示例
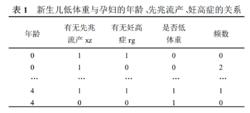
某研究者欲研究新生兒出生低體重與孕婦的年齡、先兆流產、妊高症的關係,共調查了997例婦女,整理後的數據見表1。調查包括孕婦的年齡age(0:<20歲;1:20~25歲;2:25~30歲;3:30~40;4:40歲以上),有無先兆流產xz(0:無;1:有),有無妊高症rg(0:無;1:有),試分析低出生體重與這些因素的關係。
 廣義加性模型
廣義加性模型分析:
該資料的特點是因變數為二分類變數 ,體重小於2500 g 為低出生體重兒 。可以採用 logistic 回歸來分析低出生體重與解釋變數年齡 、先兆流產 、妊高症的關係 ,但是從醫學背景考慮 ,年齡較小與年齡較大的孕婦可能發生低體重的新生兒多 ,要使這種複雜的非線性關係直觀地呈現 ,我們用半參數 logistic 廣義可加模型擬合 ,變數 xz、rg 以參數形式 ,年齡 age 用光滑樣條來擬合 。
