內容
庫塔-儒可夫斯基後緣條件
根據Kutta、儒可夫斯基升力環量定律,對於定常、理想、不可壓流動,在有勢力作用下,直均流繞過任意截面形狀的有環量繞流,翼型所受的升力為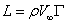
需要說明的是,不管物體形狀如何,只要環量值為零,繞流物體的升力為零;對於不同的環量值,除升力大小不同外,繞流在翼型上前後駐點的位置不同。這就是說對於給定的翼型,在一定迎角下,按照這一理論繞翼型的環量值是不定的,任意值都可以滿足翼型面是流線的邊界條件。但實際情況是,對於給定的翼型,在一定的迎角下,升力是唯一確定的。這說明對於實際翼型繞流,僅存在一個確定的繞翼型環量值,其它均是不正確的。那么,如何確定這個環量值,可從繞流圖畫入手分析。
當不同的環量值繞過翼型時,其後駐點可能位於上翼面、下翼面和後緣點三個位置的流動圖畫。後駐點位於上、下翼面的情況,氣流要繞過尖後緣,勢流理論得出,在該處將出現無窮大的速度和負壓,這在物理上是不可能的。因此,物理上可能的流動圖畫是氣流從上下翼面平順地流過翼型後緣,後緣速度值保持有限,流動實驗也證實了這一分析,Kutta、儒可夫斯基就用這一條件給出確定環量的補充條件。
庫塔-儒可夫斯基後緣條件表達
庫塔-儒可夫斯基後緣條件表達如下:(1)對於給定的翼型和迎角,繞翼型的環量值應正好使流動平滑地流過後緣去。
(2)若翼型後緣角>0,後緣點是後駐點。即V1=V2=0。
(3)若翼型後緣角=0,後緣點的速度為有限值。即V1=V2=V<>0。
(4)真實翼型的後緣並不是尖角,往往是一個小圓弧。實際流動氣流在上下翼面靠後很近的兩點發生分離,分離區很小。所提的條件是p1=p2 V1=V2
環量的產生與後緣條件的關係
根據海姆霍茲旋渦守衡定律,對於理想不可壓縮流體,在有勢力作用下,繞相同流體質點組成的封閉周線上的速度環量不隨時間變化。dG/dt=0。翼型都是從靜止狀態開始加速運動到定常狀態,根據旋渦守衡定律,翼型引起氣流運動的速度環量應與靜止狀態一樣處處為零,但庫塔條件得出一個不為零的環量值,這是乎出現了矛盾,如何認識呢。環量產生的物理原因如何。為了解決這一問題,在翼型靜止時,圍繞翼型取一個很大的封閉曲線。(1)處於靜止狀態,繞流體線的速度環量為零。(2)當翼型在剛開始啟動時,因粘性邊界層尚未在翼面上形成,繞翼型的速度環量為零,後駐點不在後緣處,而在上翼面某點,氣流將繞過後緣流向上翼面。隨時間的發展,翼面上邊界層形成,下翼面氣流繞過後緣時將形成很大的速度,壓力很低,從有後緣點到後駐點存在大的逆壓梯度,造成邊界層分離,從產生一個逆時針的環量,稱為起動渦。
(3)起動渦離開翼緣隨氣流流向下游,封閉流體線也隨氣流運動,但始終包圍翼型和起動渦,根據渦量保持定律,必然繞翼型存在一個反時針的速度環量,使得繞封閉流體線的總環量為零。這樣,翼型後駐點的位置向後移動。只要後駐點尚未移動到後緣點,翼型後緣不斷有逆時針旋渦脫落,因而繞翼型的環量不斷增大,直到氣流從後緣點平滑流出(後駐點移到後緣為止)為止。
結論
由上述討論可得出:(1)流體粘性和翼型的尖後緣是產生起動渦的物理原因。繞翼型的速度環量始終與起動渦環量大小相等、方向相反。
(2)對於一定形狀的翼型,只要給定繞流速度和迎角,就有一個固定的速度環量與之對應,確定的條件是庫塔條件。
(3)如果速度和迎角發生變化,將重新調整速度環量,以保證氣流繞過翼型時從後緣平滑匯合流出。
(4)代表繞翼型環量的旋渦,始終附著在翼型上,稱為附著渦。根據升力環量定律,直勻流加上一定強度的附著渦所產生的升力,與直勻流中一個有環量的翼型繞流完全一樣。
歷史
Kutta(1867-1944),德國數學家,1902年提出翼型繞流的環量條件。儒可夫斯基(1847-1921),俄國物理學家,1906年獨立提出該條件。
