基本介紹
通常,試驗中所研究的指標會受到諸多因素的影響。如果在試驗時,只考慮對指標影響最大的因素的變化對指標的影響,保持其他因素不變,則稱為單因素問題或單因素試驗。單因素優選法就是用儘可能少的試驗次數儘快地找到某一因素的最優值。
 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法設 為定義在區間 的單峰函式,有唯一的極大值或極小值(即最優值)。
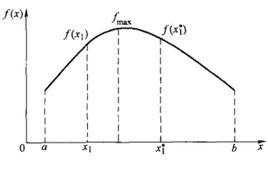
![圖1 區間[a,b]內單變數單峰函式以f(x)](/img/7/303/wZwpmL0YTNzMTO3IDMxYjN1UTM1QDN5MjM5ADMwAjMwUzLyAzLyAzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 圖1 區間[a,b]內單變數單峰函式以f(x)
圖1 區間[a,b]內單變數單峰函式以f(x) 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法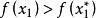 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法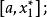 序貫試驗法
序貫試驗法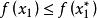 序貫試驗法
序貫試驗法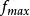 序貫試驗法
序貫試驗法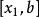 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法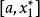 序貫試驗法
序貫試驗法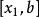 序貫試驗法
序貫試驗法如圖1所示,設 在區間 有一個極大值 。在區間內取兩試驗點 ,且 。如果 ,則 必位於區間 而如果 ,則 必位於區間 內。這樣經過一輪試驗後,最優值存在的搜尋區間便由 縮小為 或 。試驗區間縮短率δ為
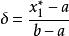 序貫試驗法
序貫試驗法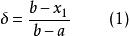 序貫試驗法
序貫試驗法或
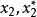 序貫試驗法
序貫試驗法在新的區間內,再取兩個試驗點,然後對試驗值進行對比。顯然這種疊代法次數越多,所在的搜尋區間越小,區間內的任一值與極大值越近似。
定義 這種根據一定的原則先安排一個或兩個試驗,然後根據前面的試驗結果再安排後面的試驗,依次進行下去,直至找到最優值的方法,稱為 序貫試驗法(Sequential experimentation)。序貫試驗法的優點是試驗總次數少,適用於單極值函式的尋優。
例 在生產鋼材時需要添加某種合金元素,合金元素含量越高,鋼材性能越高。為了降低鋼材成本,希望在使鋼材性能依然符合要求的前提下,減少合金元素加入量,如何安排試驗呢?可以在合金元素含量的允許範圍內取一點做試驗,如果鋼材性能能夠滿足要求,則可去掉比試驗點高的含量範圍,而在留下的範圍里進行進一步試驗;反之,則去掉比試驗點低的含量範圍。又如,在砂型鑄造時,開箱越早鑄件越容易出現變形和裂紋。要在確保鑄件不產生裂紋和變形的前提下,希望打箱時間越早越好。可以在開箱時間的允許範圍內取一點做試驗,如果鑄件沒有產生裂紋和變形,則可去掉比試驗點長的時間範圍,而在縮短後的時間範圍里進行進一步試驗;反之,則去掉比試驗點短的時間範圍 。
常用的序貫試驗法
常用的序貫試驗法有對分法、0.618法、分數法、拋物線法、爬山法和分批試驗法等。下面舉兩例,其他可參考相關詞條。
對分法
解決上述的鋼材合金元素含量與鑄件開箱時間問題時,可用對分法(Bisection method)選取試驗點。對分法就是總是在含優試驗範圍的中點安排試驗點,將試驗範圍對分為兩部分,根據中點的試驗結果確定取捨哪一部分。然後再在縮小後的含優試驗範圍的中點做下次試驗,如此循環直至獲得滿意結果為止。對分法也叫做平分法。顯然,對分法試驗區間縮短率6恆為0.5,每次試驗可縮短試驗範圍一半,取點非常方便。
對分法的試驗步驟概括如下:
 序貫試驗法
序貫試驗法1)首先根據經驗或預試驗確定試驗範圍[0,b]。
 序貫試驗法
序貫試驗法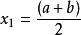 序貫試驗法
序貫試驗法2)第一次試驗在的中點做。
 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法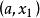 序貫試驗法
序貫試驗法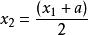 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法 序貫試驗法
序貫試驗法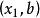 序貫試驗法
序貫試驗法3)根據試驗結果好壞確定下次試驗的位置。如果試驗結果表明取大了,則去掉大於的一半,第二次試驗在的中點處進行;如果第一次試驗結果表明取小了,則去掉以下的一半,第二次試驗取在的中點進行。
4)重複步驟3)。如此繼續下去,就可以很快地找到最優點。
套用對分法需要滿足以下兩個條件:一是要有一個標準或具體指標來鑑別試驗結果的好壞。如鋼材性能不能低於某一數值;開箱後鑄件不能出現裂紋和變形等。二是要預知該因素對指標的影響規律,即能夠從試驗結果直接判斷出該因素的值是過大還是過小。如合金元素含量越高,鋼材性能越好;開箱越早,鑄件越容易出現變形和裂紋。否則就不能確定捨棄哪段,保留哪段,也就無從下手做下一次試驗 。
0.618法
對分法中試驗點的選擇總是位於試驗區間的中點。而在0.618法中,黃金分割在試驗點的選擇上起著關鍵作用。從數學的角度來講,0.618法(Golden section method)就是把任意一條長為l的直線段分割成兩部分,其中一部分的長為0.618l。因此0.618法也稱為黃金分割法。
簡單地講,0.618法的要點是先在試驗範圍的0.618處做一次試驗,再在其對稱點即0.382處做第二次試驗;比較兩點的試驗結果,去掉含有“劣”點的部分,保留含有“優”點的部分;然後在留下部分繼續取已試點的對稱點進行試驗,再比較,通過舍劣取優,逐步縮小試驗範圍,直至取得滿意的結果。因此,可以用較少的試驗次數迅速找到最佳點。
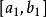 序貫試驗法
序貫試驗法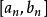 序貫試驗法
序貫試驗法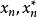 序貫試驗法
序貫試驗法設試驗的初始區間為,疊代n次的搜尋區間變為。根據0.618法的原理,每次試驗點:的選取應滿足下式:
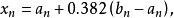 序貫試驗法
序貫試驗法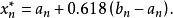 序貫試驗法
序貫試驗法套用0.618法,每次可以去掉試驗範圍的0.382倍,即0.618法的試驗區間縮短率δ為0.382。
0.618法具有試驗次數少、精度高、簡單、直觀、有效,節省人力、物力、財力等優點。因此0.618法在工業、農業、電子、化工和科學研究等領域得到了廣泛的套用 。