概念
幾乎分離集簇(almost disjoint family)簡稱adf。劃分概念的推廣。設A為一個非空集合，|A|=κ，P⊂P(A)(P(A)表示A的冪集)，若ᗄX∈P(|X|=κ)，且對任何X，Y∈P，|X∩Y|<κ，則稱P為A的幾乎分離集簇。顯然，若P中的元素兩兩分離且P=∪A，則P為A的一個劃分。若P為A的一個幾乎分離集簇，且不存在A的一個幾乎分離集簇P′真包含P，則稱P為A的最大幾乎分離集簇，記為madf。幾乎分離集簇的概念由波蘭數學家謝爾品斯基(Sierpiski，W.)於1928年引入。
劃分
劃分是形式邏輯術語。指揭示概念外延的一種邏輯方法。它是按一定標準把一個概念的外延A分成若干互不相容的並列下位概念的外延A之並。即對每一i∈I，A≠，對於每一對i，j∈I，當i≠j時，則：
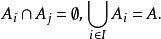幾乎分離集簇例如，三角形分為銳角三角形、直角三角形與鈍角三角形。劃分是由劃分的母項、劃分的子項和劃分的標準(根據)三個要素組成。被劃分的概念稱為劃分的母項；劃分後所得的概念稱為劃分的子項；劃分時所依據的屬性即為劃分的標準或稱劃分的根據。
形式邏輯中的劃分比數學中的劃分涵義要強一些。即要求劃分的子項是並列下位概念的外延，不是上位概念的任意非空子集。劃分也不同於分解。分解是把一個具體事物分成許多部分，而這些部分不必有由它組成的事物的整體的特有屬性。例如，把三角形分解為三條邊，其中任何一條邊都不再具有三角形的特有屬性，因此，不能說邊是三角形。而劃分則是屬與種的關係。劃分出來的各子項(種)都必須具有母項(屬)的特有屬性。例如，把大學教師分成助教、講師、教授，這裡不管助教、講師或教授都具有大學教師的特有屬性。
正確的劃分必須遵守劃分規則：
1.劃分應當是相應相稱的，即劃分的子項的外延之和等於母項的外延。
2.劃分的各個子項應當是互不相容的。
3.每次劃分必須按同一划分標準進行。
4.劃分應當按照層次進行，不應跳躍劃分。
正確的劃分能使人們明確概念的外延，了解和掌握概念適用的範圍，對於準確地理解概念和使用概念有著重要的意義。
形式邏輯
研究正確思維(概念、判斷或命題、推理)的形式結構、規律、方法和套用的科學.其主要研究對象是演繹推理的形式.“邏輯”一詞來源於希臘文λóγos(邏各斯)，原意主要指思想、言辭、理性、規律等.“形式邏輯”這一名稱最初由康德(Kant，I.)在《純粹理性批判》一書中提出，指從亞里士多德(Aristotle)到中世紀這一段時期內建立起來的邏輯科學.康德認為：形式邏輯的特點是抽掉思維的具體內容，只考察思維的形式.後來，形式邏輯有了新發展，產生了用數學方法研究邏輯的新學科——數理邏輯.因此，人們把形式邏輯分為傳統的形式邏輯(或傳統邏輯)和現代形式邏輯(或數理邏輯)兩種.習慣上，傳統的形式邏輯簡稱形式邏輯。
形式邏輯所研究的思維形式，指思維的存在和表現的形式。思維或是形成概念，或是進行判斷，或是進行推理。思維就是以概念、判斷(命題)、推理這幾種形式表現出來的。思維的形式結構就是思維的各個組成部分的聯繫方式。概念是思維的細胞。因此，思維形式結構也就是概念在判斷中的聯繫方式，判斷在複合判斷和推理中的聯繫方式，以及概念、判斷、推理在更複雜的思維中的聯繫方式等。形式邏輯研究概念的外延間的種種關係，概念內涵和外延間的關係；研究判斷的形式結構所體現的一般含義，它們的真值情況和它們之間的真值關係；以及研究推理有效性的形式準則，從而揭示思維的規律和規則。其中，最基本的規律是同一律、矛盾律、排中律和充足理由律等。形式邏輯從形式方面給思維提出規範和要求.遵守這些要求，思維就能達到形式正確性，而形式正確性是思維正確性的必要條件。因此，形式邏輯是一門教給人們正確地進行思維，識別論斷中的邏輯謬誤，以及如何準確有效地表達自己思想的科學，是一切其他科學的基礎。因此，德·摩根(De Morgan，A.)說：“數學和邏輯是精確科學的兩隻眼睛”。皮爾勒(Pierre，B.)則說：“邏輯是不可戰勝的，誰反對邏輯，誰就要用到邏輯.”形式邏輯除了以思維形式結構及其規律為主要研究對象外，還研究一些簡單的邏輯方法，如定義、劃分、分析、綜合、實驗、假說等，它們和思維形式結構及其規律有著密切的聯繫。
形式邏輯又是一門古老的科學，迄今已有兩千多年的歷史，其內容和方法都在不斷變化和發展。形式邏輯在西方產生於古希臘時期。古代的中國和古印度差不多同時期也進行了對邏輯問題的研究。中國春秋戰國時期在關於名詞(名)與其所代表的事物(實)的關係的討論中，公孫龍、惠施、墨翟和荀況等人對邏輯問題都作過研究.亞里士多德是形式邏輯的奠基人。他的主要邏輯著作《工具論》對概念、判斷、推理(主要是直言三段論)和證明都做了系統的論述，並在另一部著作《形上學》中，對矛盾律、排中律等形式邏輯的基本規律作了較詳細的討論。後來的斯多噶學派主要研究了假言推理和選言推理的理論，豐富和發展了形式邏輯。中世紀，邏輯主要發展了詞項理論和推導學說，研究了悖論問題，提出種種語義悖論和解決悖論的方法。17世紀之後，隨著實驗科學的發展，近代歸納邏輯發展起來。1620年，培根(Bacon，F.)在他的著作《新工具》中奠定了近代歸納邏輯的基礎。
近代，演繹邏輯更有新的突破。特別是從萊布尼茨(Leibniz，G.W.)到布爾(Boole，G.)，他們套用數學方法研究邏輯，從而產生了數理邏輯這門新學科。數理邏輯開始套用於數學基礎的研究，如公理方法及其有關證明，並取得巨大成果。20世紀30年代以來，數理邏輯又有了新發展，其套用範圍不斷擴大，並日益顯示出它的重要性。數理邏輯的迅速發展，改進、充實和豐富了形式邏輯的內容和方法，使其進一步適應現代科學思維發展水平。
謝爾品斯基
波蘭數學家。生於華沙，卒於同地。1899年就學於華沙大學，是俄國數論專家沃羅諾伊(Voronoi，G.)的學生，1903年因數學成績優異榮獲該校數學物理金質獎章，1906年獲博士學位，相繼在利沃夫和華沙等地的中學和大學任教。第二次世界大戰中在莫斯科羈留期間曾與盧津等原蘇聯數學家有過接觸。1945年回到華沙，先後擔任過波蘭科學院和12所外國科學院院士或通訊院士，得到過十幾所大學、研究院或數學會的職銜。此外，他曾參與創辦《數學基礎》雜誌(1920)，榮獲過波蘭一等科學獎(1949)，還培養了大批優秀數學家。謝爾品斯基是波蘭數學學派的創始人之一，共發表或出版700多篇論著，主要探討集合論和數論，給出許多重要定理，有些以他的名字命名。其中對數學影響較大的專著有《連續統假設》(1934)、《基數與序數》(1958)、《初等數論》(1964)等。他還恢復出版了國際性的數論雜誌《算術學報》，並任主編。此外，在拓撲學研究中曾給出以其名字命名的一類圖形，如面積為零的“謝爾品斯基三角形”，體積為零而表面積無窮大的“謝爾品斯基四面體”等。人們在現代分形理論的研究中，發現這些圖形都是典型的分形集。
