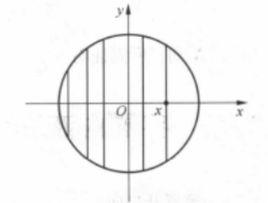
圓的平行弦
平行弦一般指圓內有特殊位置關係的兩條弦，指圓中的兩條平行弦，它們所夾的弧相等，反之，在同圓中，若兩弦所夾的圓弧相等，則此兩弦為平行弦，或者說連結圓中二等弧端點的不相交的弦是平行弦 。
例 求半徑為R的圓內平行弦長度L關於它與平行直徑距離的平均值。
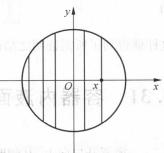圖1解 取圓心為坐標原點，垂直於平行弦的直線為x軸，建立直角坐標系如圖1所示，則圓周的方程為
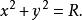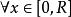平行弦
平行弦根據對稱性，我們可以只考慮右半圓，即x>0的情況， ，對應於該點的弦AB之長為
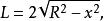平行弦所以其平均值為
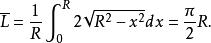平行弦注 對於求具體函式在具體區間上的平均值問題，由於函式明確、區間也明確，所以應該是沒有什麼歧見的。
但是對於求解此類套用題時，我們一定要搞清楚什麼是自變數，這樣也就能夠正確地確定出所在區間以及函式關係，否則結論將會大相逕庭 。
例如，我們同樣求半徑為R的圓內平行弦長度L的平均值，但是若求的是關於它對圓心張角θ的平均值，則由於(也只考慮右半圓)
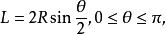平行弦所以其平均值為
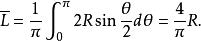平行弦二次曲線的平行弦
定理 二次曲線的平行弦中點在同一條直線上。
定義 二次曲線的一組平行弦中點所在的直線，叫做這條二次曲線的共軛於這組平行弦的直徑(也叫這組平行弦的共軛直徑)，簡稱二次曲線的直徑。而這組平行弦，叫做這條直徑的共軛弦。平行弦的方向，叫做與其共軛的直徑的共軛方向 。
顯然，二次曲線的直徑平分它的一組共軛弦。
(1) 橢園的平行弦中點的軌跡是橢園的一條直徑(所謂橢園的直徑，指橢園的過中心的弦)。
(2) 雙曲線的平行弦中點的軌跡，或是過中心的直線；或是過中心的直線上兩條關於中心對稱的射線。
(3) 拋物線的平行弦中點的軌跡，是平行於拋物線對稱軸的一條射線 。
二次曲面的平行弦
當直線和二次曲面相交時，除直線全部在二次曲面上以外，交點不能多於兩個。我們把這兩個交點所連的線段，稱為 二次曲面的弦。二次曲線的任一組平行弦的中點在一直線上，正因為如此，我們就把二次曲線平行弦中點的軌跡叫做二次曲線的直徑。二次曲面上所有平行弦中點的軌跡是一個平面，我們把這個平面稱為 二次曲面的徑面。
二次曲面的平行弦中點所構成的平面叫做這個二次曲面的共軛於這組平行弦的徑面，而這組平行弦叫做這個徑面的共軛弦。平行弦的方向，叫做這個徑面的共軛方面。
顯然，二次曲面的徑面，平分它的共軛弦。
定理 有心二次曲面的徑面都過曲面的中心。
